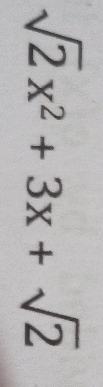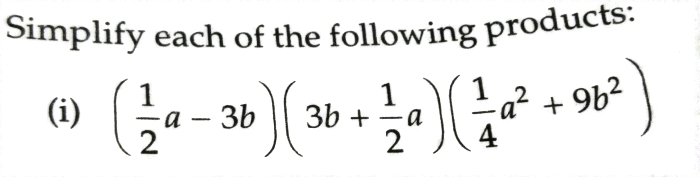CBSE Class 9 Answered
factor & remainder theorem
Asked by PraNaTi SinGh | 16 Sep, 2013, 10:24: PM
The remainder theorem is a shortcut way of finding the remainder when a polynomial is divided by (x - a). In the polynomial substitute "a" for "x" and evaluate. The result is the remainder. This saves you the effort of doing synthetic division (or long division).
The factor theorem is similar to the remainder theorem. The difference is that after you substitute "a" for "x"; if the result is 0, then (x-a) is a factor of the polynomial and "x=a" is a solution to the equation: polynomial = 0.
Or in simple words,
The correct difference between remaider theorem and factor theorem is that when the remainder is 0, it is called to be a factor theorem and when a remainder is any number, for example, 2, it is called as remainder theorem.
Answered by | 19 Sep, 2013, 10:23: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by durgavenkatlakshmi1 | 20 Mar, 2024, 03:56: PM
CBSE 9 - Maths
Asked by ammudeep0123 | 20 Mar, 2024, 07:13: AM
CBSE 9 - Maths
Asked by jaswanthsompi12345 | 19 Dec, 2023, 06:54: PM
CBSE 9 - Maths
Asked by rizwanmunna406 | 12 Dec, 2023, 10:09: PM
CBSE 9 - Maths
Asked by sathishdoddamudigere2 | 01 Nov, 2023, 06:53: PM
CBSE 9 - Maths
Asked by shambhushanker123 | 29 Oct, 2023, 08:36: PM