CBSE Class 11-science Answered
Explain apparent weight of a man in a lift.
Asked by Anvita Chaudhary | 25 Sep, 2013, 09:24: PM
A person with mass, m, who is located at or near the surface of the Earth will always have someweight W=mg. When a person stands on a scale, the reading (the number of pounds or newtons)on the scale is actually the Normal Force that the scale exerts back towards the person to supportthe person's weight. (Note that the person and the scale are stationary relative to each other, inother words they are always in contact with each other, so they always have equal and oppositeaction and reaction forces acting between them.) Things get complicated, though, when the scale and the person experience acceleration. Thiswill change the contact force (the Normal Force) between the person and the scale.Let's look at several cases. We will assume that Up is the positive direction and Down is thenegative direction.
Case 1: No acceleration of elevatorIf the acceleration of the elevator is zero, then there are two possiblescenarios; the elevator can be at rest (stationary, zero velocity) or movingwith a constant speed (no acceleration if velocity does not change).In this case, the action and reaction force pair between the person and thescale is just the weight. The person pushes down on the scale with a force of-W=-mg (negative direction) and the scale pushes back up against the manwith a Normal Force of FN = +W = +mg. Because the reading on the scale isthe magnitude of the normal force, the scale will read the true weight whenthe elevator is NOT accelerating.
Case 2: going up & speeding up (acceleration a is positive (up))In this case, the elevator and the person are starting from rest at a lowerfloor. The elevator accelerates upward. The inertia of the person wouldprefer to stay stationary, so the elevator floor and scale must push up onthe person to accelerate him upward along with the elevator. (The persondoesn't sink into the floor when the elevator accelerates up. The elevatorand the scale and the person all move together.) The scale therefore has to push upward with extra force on the person toaccelerate the person's mass upward. This results in a greater contactforce between the scale and the person. Therefore the Normal Force islarger, so the reading on the scale is a number that is GREATER than thetrue weight.Let's consider Newton's 2nd Law (?F=ma) acting on the person. The overall acceleration of theperson is upward (with the elevator). So ma is positive (upward). The only external forcesacting on the person are the force of gravity acting down (-W=-mg) and the supporting NormalForce FN that the scale applies upward on the person. So ?F=ma= -mg+FN . We want to knowFN because that is the number that we read off the scale. FN =mg+ma, which is GREATER thanthe true weight
.Case 3: going up & slowing down (acceleration a is negative (down))In this case, the elevator and the person are initially moving upward at aconstant speed and slowing down to rest at a higher floor. Theacceleration of the elevator is downward (opposite to the upward motion,which causes a reduction of the velocity). The inertia of the personwould prefer to keep moving upward at a constant speed, so the elevatorfloor and scale effectively drop out a little bit from underneath the personas the elevator slows down. The person doesn't float upward, because again the elevator and theperson move together, but the contact force between the person and thescale is reduced. The scale therefore has to push upward with less forceon the person to support the person's weight. Therefore the Normal Force is smaller, so thereading on the scale is a number that is LESS than the true weight.Let's consider Newton's 2nd Law (?F=ma) acting on the person. The overall acceleration of theperson is downward (with the elevator). So ma is negative (downward). The only externalforces acting on the person are the force of gravity acting down (-W=-mg) and the supportingNormal Force FN that the scale applies upward on the person. So ?F= -ma= -mg+FN . We wantto know FN because that is the number that we read off the scale. FN =mg - ma, which is LESSthan the true weight.
Case 4: going down & slowing down (acceleration a is positive (up))In this case, the elevator and the person are initially moving downward ata constant speed and then slow to rest at a lower floor. The elevatoraccelerates upward (opposite direction to negative/downward velocity toreduce velocity magnitude). The inertia of the person would prefer tokeep moving downward at the constant speed, so the elevator floor andscale must push up on the person to accelerate him upward, slowing himdown. (The person doesn't sink into the floor here either. Elevator andscale and person move together.)The scale therefore has to push upward with extra force on the person toaccelerate the person's mass upward. This results in a greater contactforce between the scale and the person. Therefore the Normal Force islarger, so the reading on the scale is a number that is GREATER than thetrue weight.Let's consider Newton's 2nd Law (?F=ma) acting on the person. The overall acceleration of theperson is upward (with the elevator). So ma is positive (upward). The only external forcesacting on the person are the force of gravity acting down (-W=-mg) and the supporting NormalForce FN that the scale applies upward on the person. So ?F=ma= -mg+FN . (Note that this isthe same equation as we got in case 2.) We want to know FN because that is the number that weread off the scale. FN =mg+ma, which is GREATER than the true weight. Case 5: going down & speeding up (acceleration a is negative (down))In this case, the elevator and the person are initially at rest at a higherfloor. The elevator then speeds up in the downward direction towards alower floor. The elevator acceleration of the elevator isnegative/downward (increasing the velocity magnitude in the downwarddirection). The inertia of the person would prefer to stay at rest, so theelevator floor and scale effectively drop out a little bit from underneaththe person as the elevator accelerates down. The person doesn't float upward here also, because again the elevator andthe person move together, but the contact force between the person andthe scale is reduced. The scale therefore has to push upward with lessforce on the person to support the person's weight. Therefore the Normal Force is smaller, so thereading on the scale is a number that is LESS than the true weight.Let's consider Newton's 2nd Law (?F=ma) acting on the person. The overall acceleration of theperson is downward (with the elevator). So ma is negative (downward). The only externalforces acting on the person are the force of gravity acting down (-W=-mg) and the supportingNormal Force FN that the scale applies upward on the person. So ?F= -ma= -mg+FN . (Notethat this is the same equation that we got for Case 3.) We want to know FN because that is thenumber that we read off the scale. FN =mg - ma, which is LESS than the true weight.Case 6: freefall (a = -g)If the elevator cable were to break, the whole elevator-scale-personsystem would all begin to accelerate downward due to the force ofgravity. All objects in freefall accelerate downward with the samemagnitude (acceleration due to gravity, g). The scale and the person arefreefalling together, so there is NO contact force (Normal Force)between the scale and the person. (When they are both falling together,there is no way that the scale can support any of the person's weight.)Note that this is a special case of downward acceleration, which wediscussed in Case 3 and Case 5. Just as in Cases 3 and 5, the apparentweight (which is zero when a=-g) is less than the true weight.
Answered by | 25 Sep, 2013, 11:47: PM
Concept Videos
CBSE 11-science - Physics
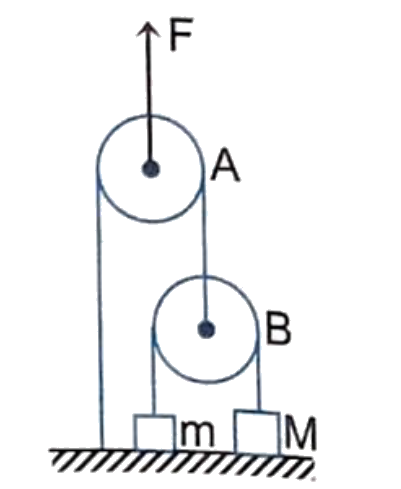
Asked by pranavsrinivas82 | 08 Jan, 2024, 11:30: PM
CBSE 11-science - Physics
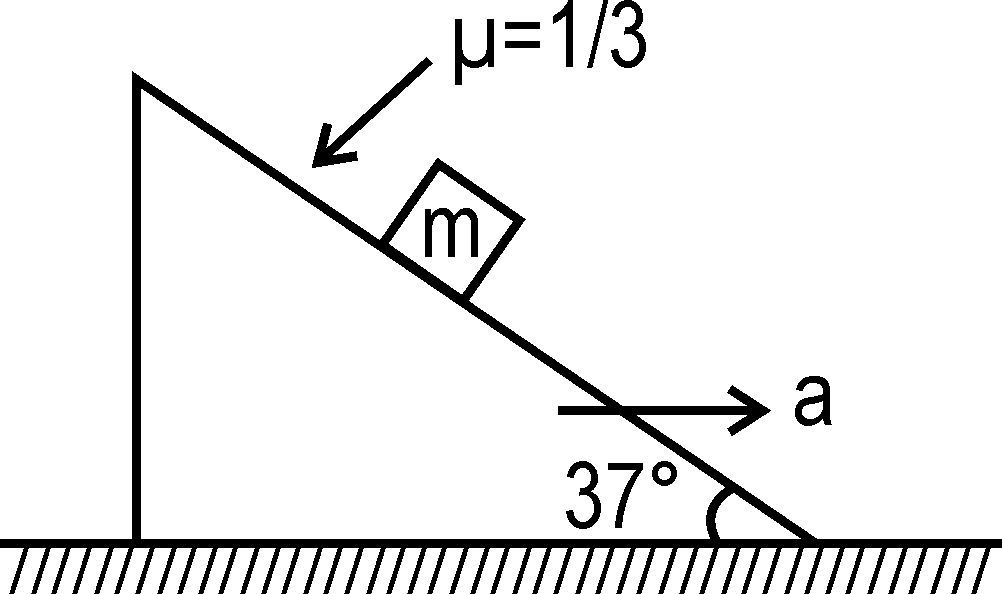
Asked by rame123shshiv | 14 Nov, 2023, 06:18: AM
CBSE 11-science - Physics
Asked by kfcispuppy | 30 Sep, 2023, 10:06: AM
CBSE 11-science - Physics
Asked by sakethrockzz007 | 14 Aug, 2023, 04:30: PM
CBSE 11-science - Physics
Asked by sahuaryanbro1.0 | 01 Jan, 2023, 10:17: PM
CBSE 11-science - Physics
Asked by subhankarnanda123 | 20 Dec, 2022, 08:36: PM
CBSE 11-science - Physics
Asked by kashyspalbert91 | 11 Mar, 2022, 04:11: PM
CBSE 11-science - Physics
Asked by alkrishna4652 | 24 Feb, 2022, 01:46: PM
CBSE 11-science - Physics
Asked by shreyamishra270304 | 04 Aug, 2021, 08:32: AM