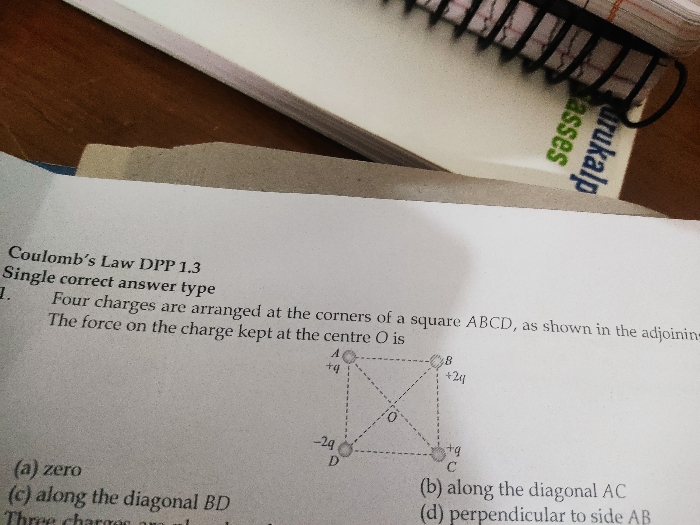JEE Class main Answered
Derive the formula for elongation of spring by its own weight?
Asked by rushabhjain.av | 28 Nov, 2019, 02:48: PM
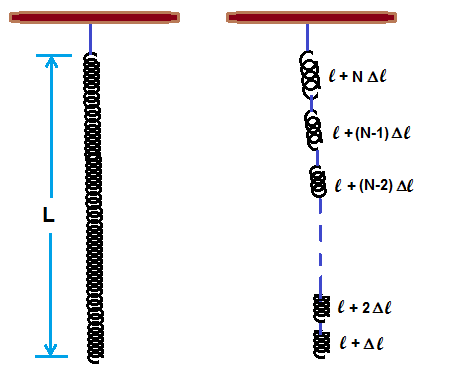
Let a long spring of length L , Mass M and spring constant K is hanged vertically as shown in figure.
Upper part of the spring experiences gretaer downward force due to more weight below
but lower part of the spring experiences less force due to less weight below. Hence elongation of spring is more
in upper part of sprin and less in lower part of spring.
Let us divide the long spring into N parts of small spring of equal length l, so that l = L/N , mass of small spring m = M/N
and spring constant of small spring k = K/N .
If Δl is the elongation of small spring due to its own weight mg, then elongated length L' of whole spring due to
elongation of each small spring starting from top can be written as,
L' = [ l + (N)Δl ] + [ l + (N-1)Δl ] + [ l + (N-2)Δl]+...................+[ l + (2)Δl] + [l + (1)Δl ] ...................(1)
L' = (N × l ) + [ N + (N-1) + (N-2) +....................+2+1 ] Δl = L + [ N (N+1) / 2 ] Δl ......................(2)
when N → ∞ , then we have N(N+1) ≈ N2
Elongation of each small spring, Δl = (mg ) / k
Using above substitution, eqn.(2) is written as, L' = L + ( N2 Δl /2 ) = L + (1/2)N2 ( mg )/k = L + (1/2)[ (N m) g / (k/N) ]
we get, L' = L + (1/2)( M g / K )
Hence net elongation = ( M g ) / ( 2 K )
Answered by Thiyagarajan K | 28 Nov, 2019, 06:06: PM
Application Videos
JEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
JEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
JEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
JEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
JEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
JEE main - Physics
Asked by mfkatagi099 | 20 Mar, 2024, 09:35: PM
JEE main - Physics
Asked by sreelekhachakali2006 | 15 Mar, 2024, 10:35: AM