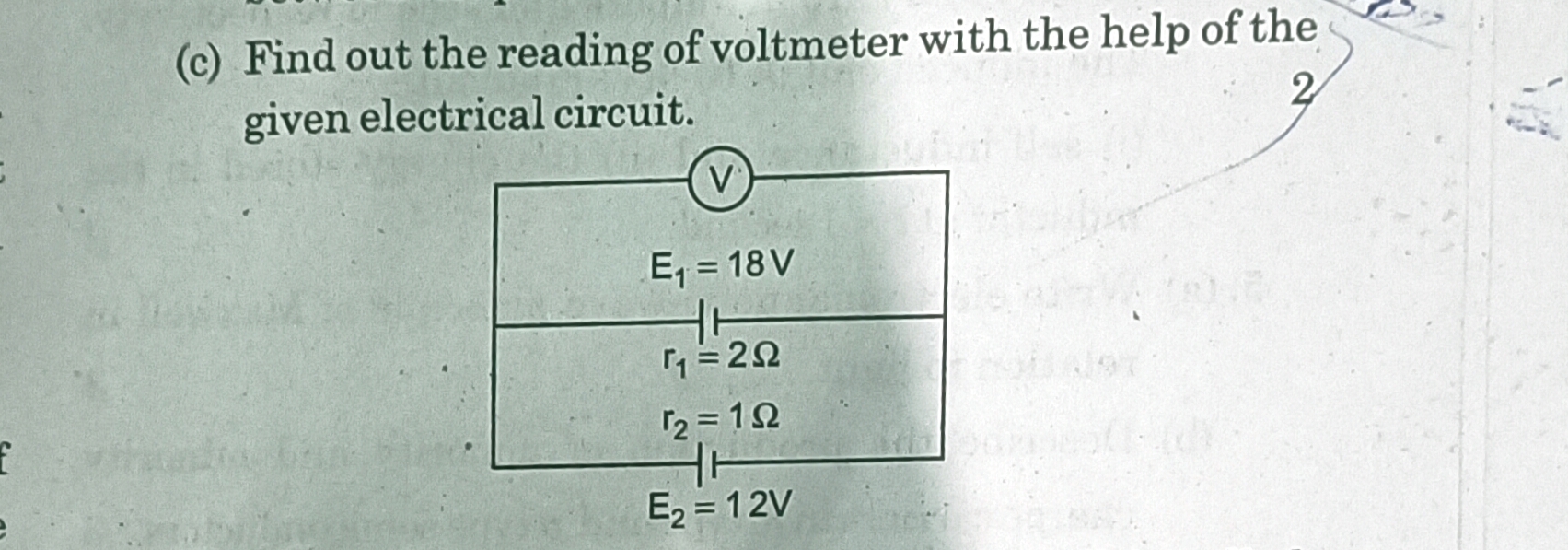
CBSE Class 12-science Answered
power transfer is maximum when r = R which means internal resistance of source equals the load resistance. It is called the maximum power theorem.
Note that we are talking about maximum power and not maximum efficiency. If resistance of the load is greater than the resistance of the source, efficiency is more but overall powr is low.
If internal impedance is made larger than the load the most of the power is dissipated in the source itself, but although the total power dissipated is higher, due to a lower circuit resistance, it turns out that the amount dissipated in the load is reduced.
This can be proved using calculus. I have copied and pasted the proof from wikipedia, url of website is also pasted for further reading.
http://en.wikipedia.org/wiki/Maximum_power_theorem
In the diagram opposite, power is being transferred from the source, with voltage V and fixed source resistance RS, to a load with resistance RL, resulting in a current I. By Ohm's law, I is simply the source voltage divided by the total circuit resistance:
The power PL dissipated in the load is the square of the current multiplied by the resistance:
We could calculate the value of RL for which this expression is a maximum, but it is easier to calculate the value of RL for which the denominator
is a minimum. The result will be the same in either case. Differentiating with respect to RL:
For a maximum or minimum, the first derivative is zero, so
or
In practical resistive circuits, RS and RL are both positive. To find out whether this solution is a minimum or a maximum, we must differentiate again:
This is positive for positive values of RS and RL, showing that the denominator is a minimum, and the power is therefore a maximum, when
- RS = RL.