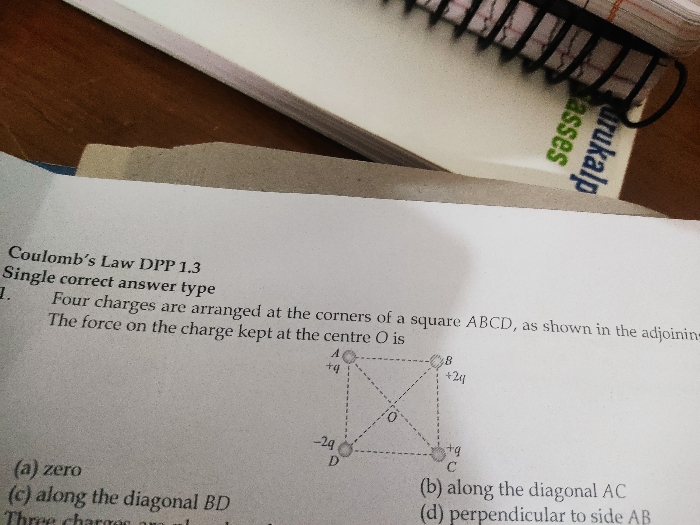JEE Class main Answered
Consider an imaginary cube with different vertices of the cube marked as shown A.point charge is placed at
the vortex H and flux through the face ABCD is x in this case. Now the charge is shifted to centroid of the
cube Flux through the five AEHD in this case is kx .What is the value of k?
Asked by sumsansam | 14 Jun, 2019, 12:19: AM
Expert Answer
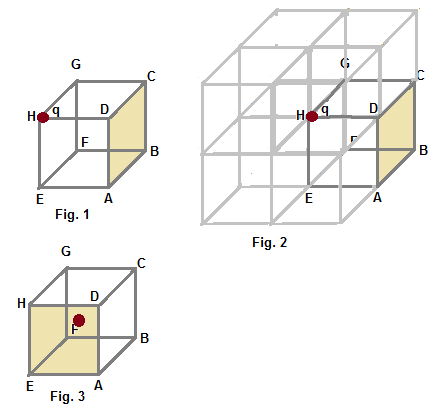
Relevant figure is not given, but I guess fig.1 is drawn as per the requirement of this question.
Electric flux through the given surface due to given charge configuration is obtained using Gauss theorem .
Total electric flux over the surface of encosure = 
where integration is done over the surface area of enclosure, E is electric field at a small surface elelemt dA,
q is the total charge inside the enclosure and ε is the electric permeability of the medium inside enclosure.
Flux calculation over the surface is simplified if enclosure is symmetrical with the the enclosed charge.
Hence to get flux through face ABCD as shown in fig.1, we make an imaginary enclosure using
8 identical cubes as shown in figure 2 so that charge q is centrally located.
Now the total flux over the surface of imaginary enclosure is ( q/ε ) V/m .
Since the flux over the surface is uniform, flux through face ABCD = (q/ε)×[a2/(24a2)] = q/(24ε) V/m ........................(1)
When the charge is shifted to the centroid of cube as shown in fig.3,
now total flux over the surface of cube is ( q/ε ) V/m .
Hence flux through the face AEHD = (q/ε)×[a2/(6a2)] = q/(6ε) V/m ..........................(2)
If we assume the electric flux given in eqn.(1) as x V/m and that of eqn.(2) as kx V/m , then we get k = 4
Answered by Thiyagarajan K | 14 Jun, 2019, 10:30: AM
Application Videos
-
Elastic potential energy_Restoring force and spring con ...
In this video, the restoring force and spring constant is explained. The vi... -
Expression of Elastic potential energy_2
This video describes the potential energy of spring when it is compressed o... -
Potential Energy Curve
This video describes the potential energy curve and ature of forces based o... -
Work done by static friction
This video describes effect of static friction on the work done by the obje... -
Work done in conservative field - 1
The concept of conservative field, types of conservative forces and example...
JEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT
JEE main - Physics
Asked by mfkatagi099 | 20 Mar, 2024, 09:35: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by sreelekhachakali2006 | 15 Mar, 2024, 10:35: AM
ANSWERED BY EXPERT
