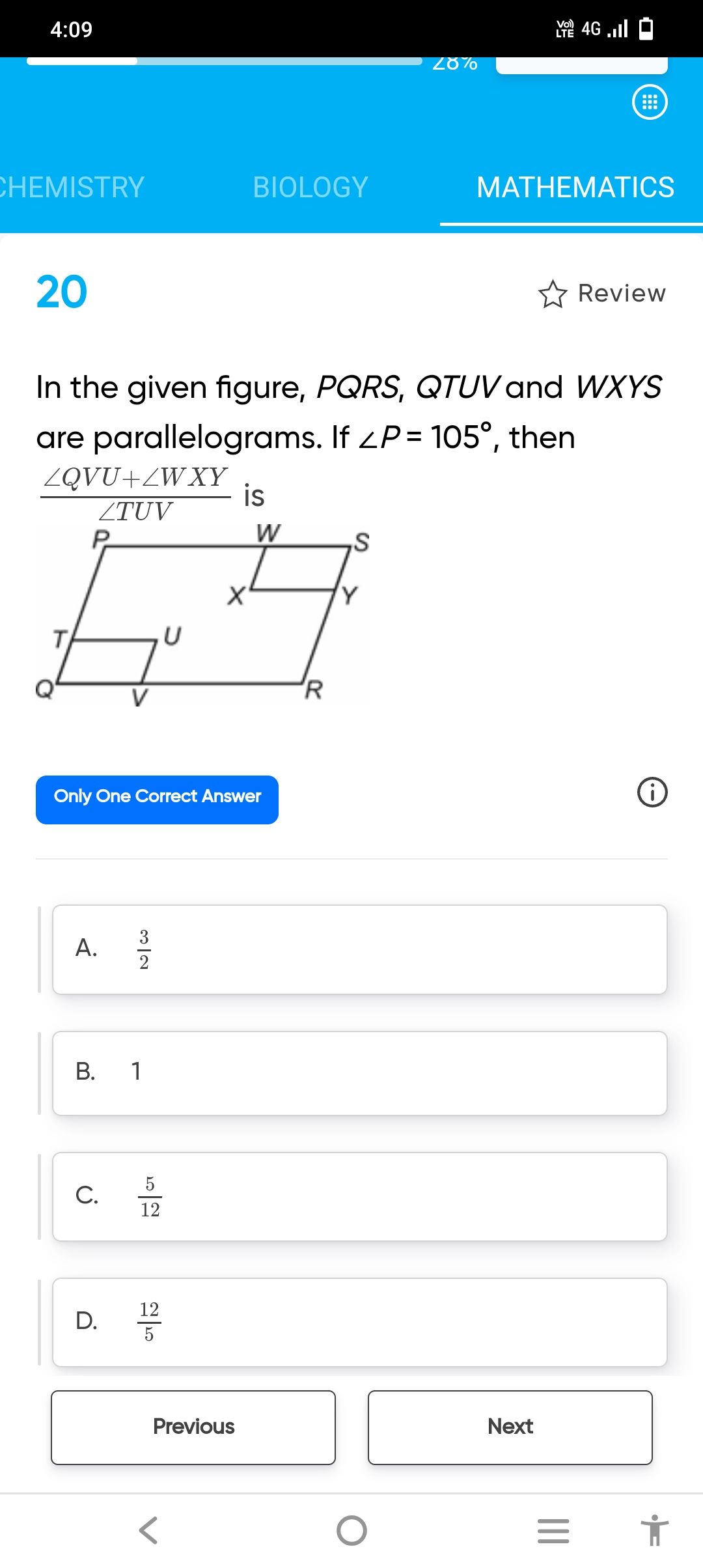
CBSE Class 9 Answered
ABCD is a square & angle PQR=90
Asked by | 01 Mar, 2013, 12:44: AM

Answer : Given : ABCD is a square & angle PQR=90 .
P,Q,R are 3 points on AB,BC & CD respectively.AP=CR.
To Prove :
1.PB = QC
2.PQ=QR
3.Angle QPR=45
Let as assume that angle QPR =a and angle QRP = b
Now , in triangle PQR and triangle QCR
angle PQR = angle QCR = 90
angle PRQ = angle RQC = b .....(1) { opposite angles}
angle QPR = angle QRC = a....(2) {exterior angles}
therefore the triangles are congruent by AAA property.
=> QR= QC .....(3)
similarily triangle PQR is congruent to triangle PBQ and as well congruent to triangle QCR
=> QC = QR = PB {using 3}
also QR = PQ {of triangle QCR and triangle PBQ } ......(4)
now eq 4 suggests that in triangle PQR PQ = QR
therefore triangle PQR is issoceles triangle
=> angle a = angle b .....(5) {angles of the issoceles triangles are equal }
Now in triangle PQR
90 + angle a+ angle b = 180
angle a+ angle b = 180 - 90 = 90
2 angle a = 90 {using eq5}
=> angle a = 45 degree
i.e angle QPR = 45 degree
Hence proved
Answered by | 06 Mar, 2013, 06:16: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
CBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
CBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
CBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
CBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
CBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
CBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
CBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM