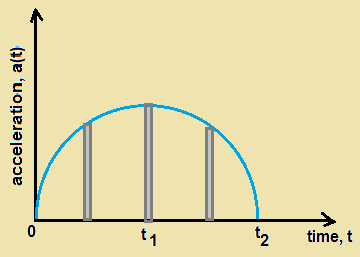
A : The acceleration-time graph for an object moving along straight line, starting from rest is as shown in figure.
Speed of the particle is maximum at time t1.
R : Velocity is maximum when acceleration is maximum.
Asked by dipanshusingla029
23rd May 2018,
5:16 PM
Answered by Expert
Answer:
We are given that acceleration is function of time.
so we have 
.....................(1)
.....................(1)where v is speed and a is acceleration
we can write velocity v as a functon of time from (1) as follows
hence v(t) , i.e. velocity at time t is area under the given curve that represent the acceleration function for a small time period dt as shown in figure.
we can see that the area under the curve having small width dt is maximum at t = t1.
hence we can conclude speed is maximum at t = t1.
Answered by Expert
25th May 2018,
12:56 PM
Rate this answer
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer 1/10
Your answer has been posted successfully!
RELATED STUDY RESOURCES :
Browse free questions and answers by Chapters
- 1 Thermodynamics
- 2 Gravitation
- 3 Electromagnetic Waves
- 4 Communication Systems
- 5 Laws of Motion
- 6 Current Electricity
- 7 Work, Energy and Power
- 8 Kinematics
- 9 Physics and Measurement
- 10 Rotational Motion
- 11 Properties of Solids and Liquids
- 12 Kinetic Theory of Gases
- 13 Oscillations and Waves
- 14 Electrostatics
- 15 Magnetic Effects of Current and Magnetism
- 16 Electromagnetic Induction and Alternating Currents
- 17 Optics
- 18 Dual Nature of Matter and Radiation
- 19 Atoms and Nuclei
- 20 Electronic Devices
Trending Tags
Latest Questions
JEE Main Mathematics
Asked by amaladelsingh
28th October 2020,
10:24 PM
CBSE X Biology
Asked by reenacharan2008
28th October 2020,
9:11 PM
