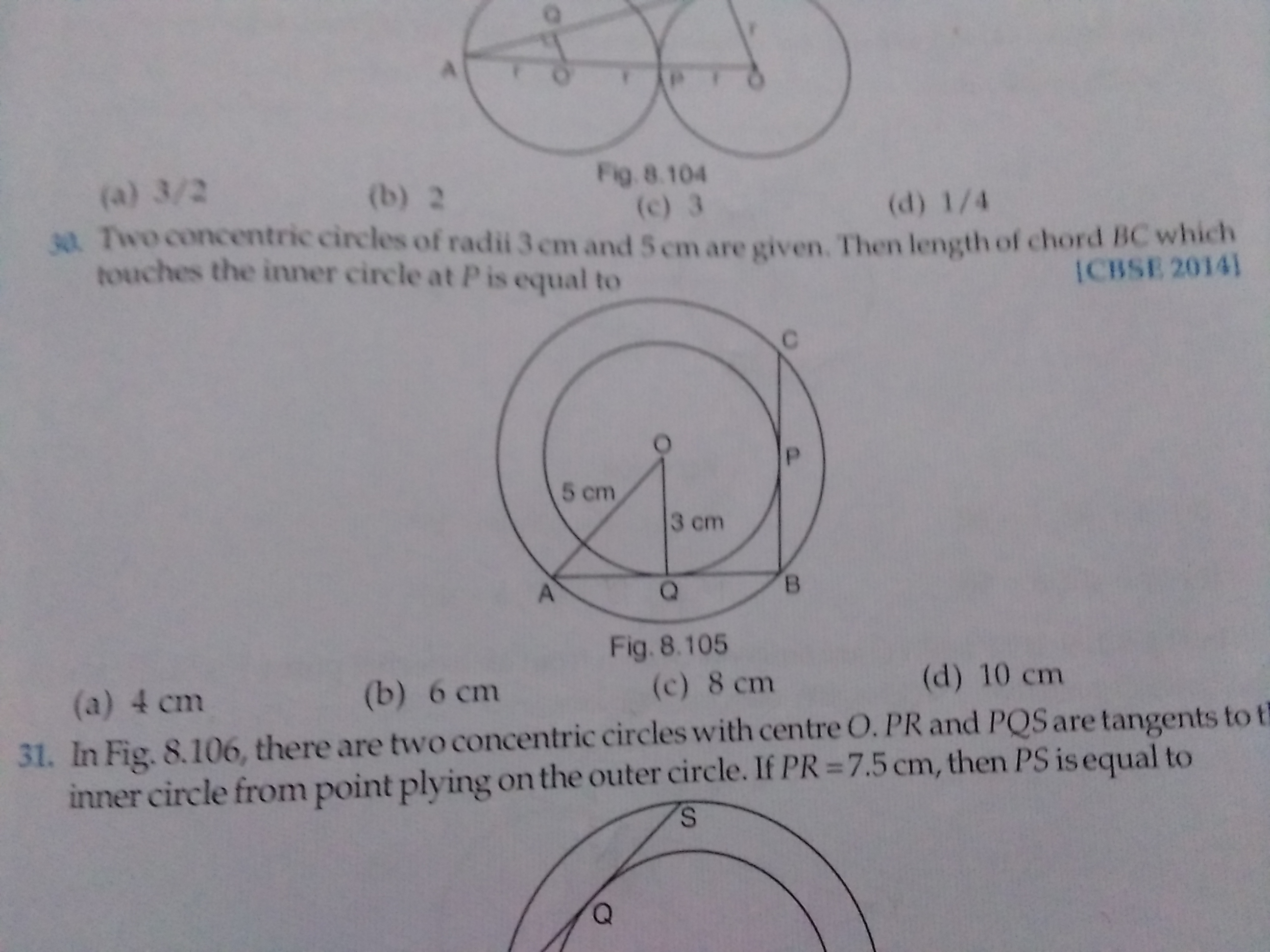
CBSE Class 10 Answered

Construction: Join PO and produce to D.

Now, OP is perpendicular TP  (tangent makes a 90 degree angle with the radius of the circle at the point of contact)

Also, TP is parallel to AB 

∴∠ADP=90° (corresponding angles)

So, OD is perpendicular to AB. Now since, a perpendicular drawn from the center of the circle

to a chord bisects it.

Hence, PD is a bisector of AB. i.e. AD = DB

Now in triangle ADP and BDP

AB =DB (proved above) 

∠ADP=∠BDP (both are 90°)

 PD = DP  (common)

⇒ΔADPΔBDP ( by SAS)

Hence, ∠PAD = ∠PBD (By CPCT)

Thus, APB is an isosceles triangle.