CBSE Class 10 Answered
A straight highway leads to foot of a tower. A man
standing at the top of the tower observes a car at an angle of depression of
30o, which is approaching the foot of the tower with a uniform
speed. Six seconds later the angle of depression of the car is found to be 60o.
Find the time taken by the car to reach the foot of the tower from this
point.
Asked by Topperlearning User | 27 Jul, 2017, 11:02: AM
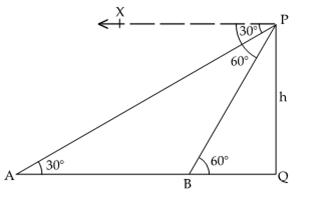
Let PQ = h metres be the height of the tower. P is the top of the tower.
The first and second positions of the car are at A and B respectively.
![]() APX
= 30o
APX
= 30o ![]() PAQ = 30o
PAQ = 30o
![]() BPX
= 60o
BPX
= 60o ![]() PBQ = 60o
PBQ = 60o
Let the speed of the car be x m/second
Then, distance AB = 6x meters
Let the time taken from B to Q be n seconds
![]() BQ = nx metres
BQ = nx metres
In ![]() PAQ,
PAQ,
![]()
![]() ...(1)
...(1)
In ![]() PBQ,
PBQ,
![]()
![]() ...(2)
...(2)
From (1) and (2),
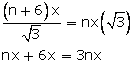
n = 3
Hence, the time taken by the car to reach the foot of the tower from B is 3 seconds.
Answered by | 27 Jul, 2017, 01:02: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by swetalinasamantaray022 | 21 Mar, 2023, 04:15: PM
CBSE 10 - Maths
Asked by badakhsharda | 14 Apr, 2022, 08:57: AM
CBSE 10 - Maths
Asked by naancysingh | 09 Apr, 2022, 07:07: PM
CBSE 10 - Maths
Asked by vy499292 | 23 Jan, 2022, 08:04: PM
CBSE 10 - Maths
Asked by urzashu7818 | 15 Jan, 2021, 12:52: PM
CBSE 10 - Maths
Asked by arindeep.singh | 11 Sep, 2020, 02:41: PM
CBSE 10 - Maths
Asked by debeswar32 | 06 Aug, 2020, 10:55: AM
CBSE 10 - Maths
Asked by ahmadaarif199 | 24 Jul, 2020, 02:58: PM











