NEET Class neet Answered

A square formed by 4 identical rods of length l and mass m .moment of inertia about x y and z axis when a side lie on x axis and other on y axis

Asked by gungunmishra102 | 10 Oct, 2019, 10:21: AM

Expert Answer

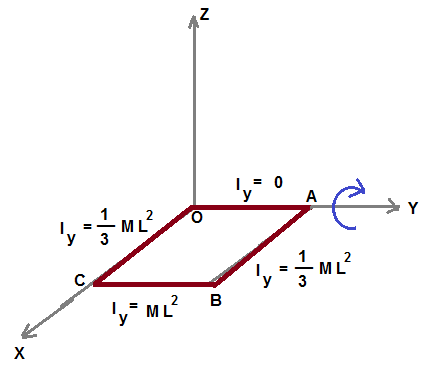
figure shows the square formed by four identical rods of length L and Mass M placed in XY plane.

Moment of inertia I_y about y axis = I_OA + I_AB + I_BC + I_OC

where I_OAis moment of inertia of rod OA abount y-axis. Similarly for others.

since roatation axis passing through OA, and rod is thin, I_OA = 0

I_AB = I_OC = (1/3)ML²

Each point of rod BC is at equal distance from rotation axis. Hence I_BC = ML²

Hence Moment of inertia about y-axis = I_y = (1/3)ML² + (1/3)ML² + ML² = (5/3)ML²

(M is mass of single rod)

Moment of inertial of x-axis is also similar to that of y-axis , hence I_x = (5/3)ML²

----------------------------------------------------------------------------------------------------------------------

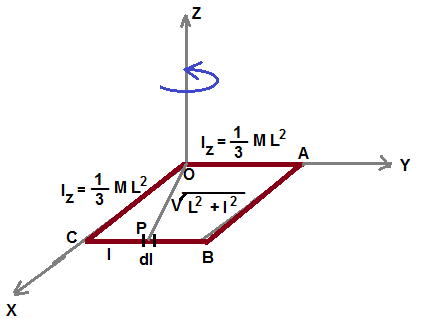
Now let us consider Moment of inertia of the square formed by four rods about z-axis

For rod OA and OC, moment of inertia is (1/3) ML²

Let us calculate the moment of inertia of rod CB.

let us consider small length dl at a distance l from one end C

Moment of inertia of small mass dm of this small length is dm (L² + l²) ( refer figure for distance)

If mass is distributed uniformly, mass per unit length is M/L. Hence mass of dl length dm = (M/L) dl

dI = dm (L² + l²) = (M/L) (L² + l² ) dl

Moment of inertia of whole rod is given by,

begin mathsize 14px style I space equals space integral d I space equals space M over L integral subscript 0 superscript L left parenthesis L squared plus space l squared right parenthesis space d l space space equals space 4 over 3 M L squared end style

Moment of inertia of rod AB is also calculated in same manner and is equal to (4/3)ML²

Hence moment of inertia of the square formed by 4 rods about z-axis,

I_z= (1/3) ML² + (1/3) ML² +(4/3) ML² +(4/3) ML² = (10/3) ML²

(M is mass of single rod)

Answered by Thiyagarajan K | 10 Oct, 2019, 03:19: PM

Application Videos