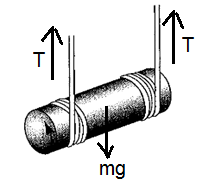
. A solid cylinder of mass m 4kg and radius
R-10cm has two ropes wrapped around it, one
near each end. The cylinder is held horizontally
by fixing the two free ends of the cords to the
hooks on the ceiling such that both the cords
are exactly vertical. The cylinder is released
to fall under gravity. Find the tension along
the strings.
1) 6.53N 2) 5.23N 3) 3.23N 4) 4.43N
. A solid cylinder of mass m 4kg and radius
R-10cm has two ropes wrapped around it, one
near each end. The cylinder is held horizontally
by fixing the two free ends of the cords to the
hooks on the ceiling such that both the cords
are exactly vertical. The cylinder is released
to fall under gravity. Find the tension along
the strings.
1) 6.53N 2) 5.23N 3) 3.23N 4) 4.43N
Asked by chandanbr6004
25th November 2017,
2:20 PM
Answered by Expert
Answer:
Let a be the acceleration when the cylinder is falling freely.
m × a = m × g - 2×T ............................(1)
Let r be the radius of cylinder. If torque acting on both the ends are similar then net torque is given by
...........................(2)Where I is moment of inertai and α is angular acceleration due to rod rotation.
if we substitute for I and α in the above equation we get
Substituting the above equation for T in eqn.(1) , we get a = (2/3)g
Hence T = (1/4)×4×(2/3)x9.8 = 6.53 N
Answered by Expert
29th November 2017,
3:46 PM
Rate this answer
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer /10
Your answer has been posted successfully!
RELATED STUDY RESOURCES :
JEE QUESTION ANSWERS
Browse free questions and answers by Chapters
- 1 Thermodynamics
- 2 Gravitation
- 3 Electromagnetic Waves
- 4 Communication Systems
- 5 Laws of Motion
- 6 Current Electricity
- 7 Work, Energy and Power
- 8 Kinematics
- 9 Physics and Measurement
- 10 Rotational Motion
- 11 Properties of Solids and Liquids
- 12 Kinetic Theory of Gases
- 13 Oscillations and Waves
- 14 Electrostatics
- 15 Magnetic Effects of Current and Magnetism
- 16 Electromagnetic Induction and Alternating Currents
- 17 Optics
- 18 Dual Nature of Matter and Radiation
- 19 Atoms and Nuclei
- 20 Electronic Devices
Trending Tags
Latest Questions
JEE Main Mathematics
Asked by amaladelsingh
28th October 2020,
10:24 PM
CBSE X Biology
Asked by reenacharan2008
28th October 2020,
9:11 PM
