CBSE Class 11-science Answered
A smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
Asked by haroonrashidgkp | 13 Feb, 2018, 09:58: PM
Expert Answer
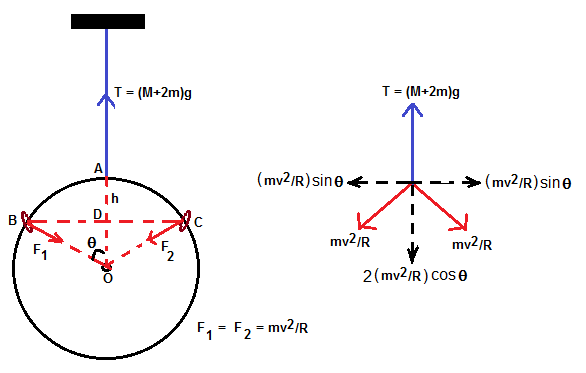
The problem is illustrated in the above diagram. Let M be the mass of circular track and m is mass of ring.
Tension T acting in the string is (M+2m)g.
Since the rings are constrained to travel in circular path, there is a centripetal force due to the movement of each ring.
Let θ is the angle made by the line joining the centre point O and the left sliding ring to the vertical as shown in figure.
Force diagram is given for this particula moment in the right side of figure.
resolved horizontal componenets of centripetal forces cancel each other, while the vertical components added up and acting against tension.
To make the tension zero, the required condition is
...........................(1)where v is the tangetial speed of ring and R is radius of circular track
if R is circular radius, distance h = R(1-cosθ)
since the rings are starting from rest and if the vertical component of the speed is v×sinθ when they reach the angular position θ, then we have
..............................(2)substituting v2 from (2) in (1), we get
Hence from the known values of M and m one can estimate the value of θ
Answered by Thiyagarajan K | 15 Feb, 2018, 03:53: PM
CBSE 11-science - Physics
Asked by sheikhsaadat24 | 17 Apr, 2024, 09:41: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by sy123946 | 07 Apr, 2024, 04:23: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by derhebha955 | 03 Apr, 2024, 09:03: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by sumedhasingh238 | 29 Mar, 2024, 05:15: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by sumedhasingh238 | 28 Mar, 2024, 11:10: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by roshnibudhrani88 | 23 Mar, 2024, 05:52: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by om636694 | 04 Mar, 2024, 09:10: PM
ANSWERED BY EXPERTCBSE 11-science - Physics
Asked by rajuinwati12 | 04 Mar, 2024, 09:22: AM
ANSWERED BY EXPERT
