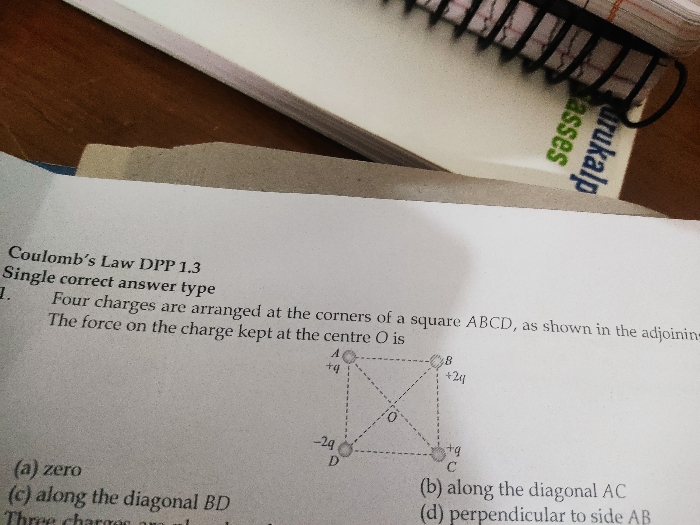JEE Class main Answered
A particle of mass m and positive charge q is projected towards an infinity long line of charge from a distance r the velocity v makes 30 degree with normal to the line charge the minimum distance of approach of charge particle with line of charge
Asked by ayushsahuopp | 21 Jan, 2020, 10:03: AM
Expert Answer
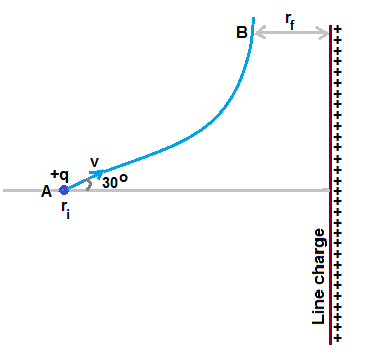
Figure shows the trajectory of charged particle moving in the electric field due to infinite line charge.
Initially the charge particle started with velocity v in the direction that makes angle 30° to the normal drawn to the infinite line charge.
If we resolve the velocity as ( v cos30 ) along the normal and ( v sin30 ) along the perpendiculardirection to normal,
then ( v cos30 ) component is affected due to force F of repulsion due to electric field of infinite line charge.
The vertical componenet ( v sin30 ) is unaffected.
Hence the charged particle move in a parabolic path like projectile motion in gravitational field.
If vi = ( v cos30 ) is the initial velocity at A along the direction of normal and the velocity becomes zero at B,
then by work-energy theorem ,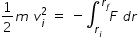 
...............................(1)
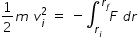...............................(1)where F is the force due to electric field 
.....................(2)
.....................(2)where λ is the charge per unit length in the infinite line charge
hence eqn.(1) is written as,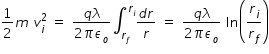 
...................(3)
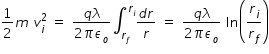...................(3)By substituting vi = ( v cos30 ) in above eqn.(3), we get , rf = ri exp[ - ( 3m v2 π εo ) / ( 4 q λ ) ]
Answered by Thiyagarajan K | 21 Jan, 2020, 11:04: PM
Application Videos
-
Elastic potential energy_Restoring force and spring con ...
In this video, the restoring force and spring constant is explained. The vi... -
Expression of Elastic potential energy_2
This video describes the potential energy of spring when it is compressed o... -
Potential Energy Curve
This video describes the potential energy curve and ature of forces based o... -
Work done by static friction
This video describes effect of static friction on the work done by the obje... -
Work done in conservative field - 1
The concept of conservative field, types of conservative forces and example...
JEE main - Physics
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT
JEE main - Physics
Asked by mfkatagi099 | 20 Mar, 2024, 09:35: PM
ANSWERED BY EXPERT
