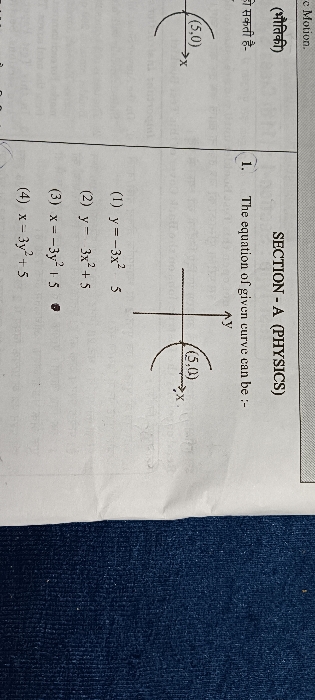NEET Class neet Answered
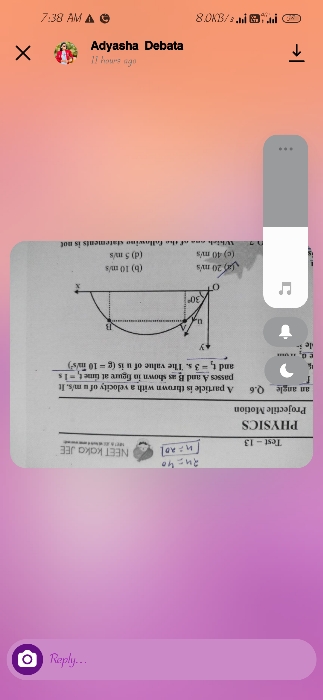
A balloon starts moving vertically upwards with a uniform acceleration of 1.25 m / s2 After 10 s a stone is dropped from the balloon then find - ( g 10 ms- 2 ) ( 1 ) maximum height from the stone
(2 ) the stone time taken to reach the ground
Asked by surabhilakhara7299 | 14 Jun, 2021, 07:54: AM
Expert Answer
Height h reached by baloon after 10 s is determined from the folowing equation
h = (1/2) a t2
where a = 1.25 m/s2 is unifor acceleration of balloon and t is time
h = 0.5 × 1.25 × 10 × 10 = 62.5 m
velocity v of balloon after 10 s , v = a × t = 1.25 × 10 = 12.5 m/s
Hence when the stone is dropped at a height of 62.5 m , it has initial velocity 12.5 m/s upward.
Maximum height H reached by stone from dropping point is determined from the following equation of motion
v2 = u2 - ( 2 g H )
where v = 0 is final velocity because stone reaches zero velocity at maximum height ,
u is inital velocity of stone and g is acceleration due to gravity.
H = u2 / ( 2 g ) = ( 12.5 × 12.5 ) / ( 2 × 10 ) = 7.8125 m
Maximum height reached by stone from ground = ( 62.5 + 7.8125 ) m = 70.3125 m
Time taken t by stone to reach ground is determined from the following equation
S = u t - [ (1/2) g t2 ]
where S = -62.5 m because stone is dropped at a height of 62.5 m above ground level ,
hence it has to reach this distance backwards.
-62.5 = 12.5 t - [ 0.5 × 10 × t2 ] = 12.5 t - 5 t2
Hence we get a quadratic equation in t , 5 t2 - 12.5 t - 62.5 = 0
By solving above quadratic equation , we get t = 5 s
Answered by Thiyagarajan K | 14 Jun, 2021, 08:37: AM
NEET neet - Physics
Asked by onemile96 | 30 Mar, 2024, 01:04: PM
ANSWERED BY EXPERT
NEET neet - Physics
Asked by kulsawran12345 | 10 Mar, 2024, 07:31: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by khillare.sonu10 | 29 Feb, 2024, 09:44: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by vijayyadav08735 | 08 Feb, 2024, 03:31: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by rkr112744 | 31 Jan, 2024, 11:18: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by divyamahaver2506 | 28 Jan, 2024, 05:54: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by ashishmishra50737 | 21 Dec, 2023, 08:07: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by studentinmalti | 10 Dec, 2023, 12:16: PM
ANSWERED BY EXPERT
