CBSE Class 9: Properties of Equal Chords Videos | Properties of Equal Chords

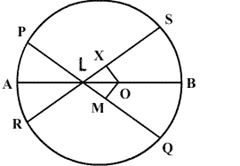
• If two intersecting chords PQ and RS of a circle make equal angles with the diameter passing through their point of intersection, then prove that the chords are equal.
• Prove that the angle in the minor segment is an obtuse angle.
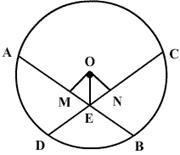
• In the given figure, equal chords AB and CD of a circle C(O, r) cut at right angles at E. If M and N are the mid points of AB and CD respectively, prove that OMEN is a square.
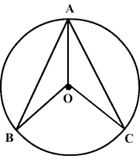
• In the figure A, B and C are three points on a circle such that the angle subtended by the chords AB and AC at the centre are 120^o and 80^o respectively. Determine angle BAC.
• P is the centre of the circle. Prove that XPZ is equal to twice the sum of XZY and YXZ.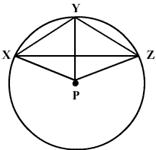
• O is the centre of the circle, find the value of x.
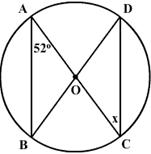
• AB and AC are two equal chords of a circle whose centre is O. If OD is perpendicular to AB and OE is perpendicular to AC, prove that ADE is an isosceles triangle.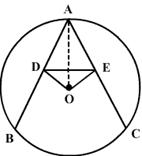
• O is the centre of the circle and PQ is a diameter. If ROS is equal to 40^o find RTQ.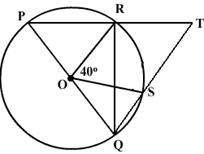
• PQ and RQ are the two chords of a circle equidistant from the centre O. Prove that the diameter passing through Q bisects PQR and PSR.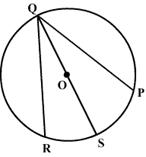
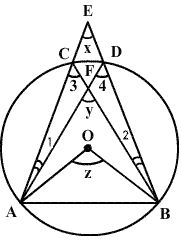
• In the figure, O is the centre of a circle. Prove that x + y = z.

Queries asked on Sunday & after 7 pm from Monday to Saturday will be answered after 12 pm the next working day.