CBSE Class 11 science: Applications of Mathematical Induction Videos | Problem solving on principles of mathematical induction

• Q-6 in the image
  
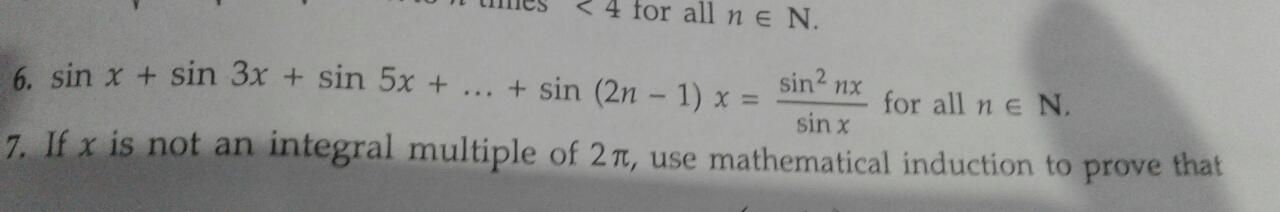
• Prove 10th by mathatical induction
  
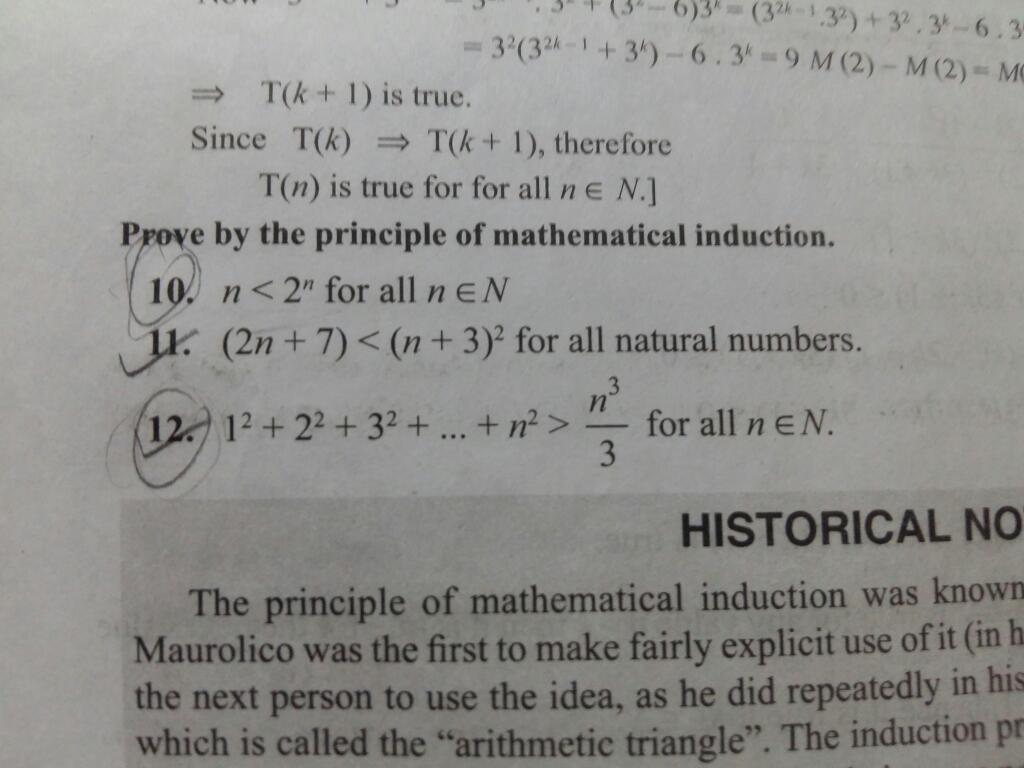
• Prove by using the principle of mathematical induction 3²ⁿ – 1 is divisible by 8 for n N.
• Prove by using the principle of mathematical induction n(n + 1)(n + 2) is divisible by 6 for all n N.
• If P(n) is the statement ‘2²ⁿ – 1 is multiple of 3’ then show that P(5) is true.
• Let P(n) be the statement," n³ + n is divisible by 3". Check whether P(3) and P(4) is true.
• Prove by using the principle of mathematical induction 3ⁿ < 4ⁿ for all n 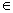N.
• If  P(n) is the statement 7²ⁿ + 2^{3n - 3}.3^{n - 1} is divisible by 25 for all n 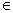N, then what is P(k + 1)?
• Show that if statement P(n): 2 + 4 + 6 + --- + 2n =  n( n + 1) + 2 is true for n = k, then it is also true for n = k + 1. Can we apply the principle of mathematical induction?
• Prove that 10^{2n – 1} + 1 is divisible by 11 for all n 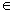N.

Queries asked on Sunday & after 7 pm from Monday to Saturday will be answered after 12 pm the next working day.