CBSE Class 11-science Maths Relation Between AM and GM

• G₁, G₂, …, G_n are n geometric means between a and b. Find common ratio and (r + 1)th term of this GP (r < n).
• Find three geometric means between the numbers 3 and 48.
• Find the numbers whose arithmetic mean is 82 and geometric mean is 18.
• Find the sum of the series 3 + 9 + 27 + ……+ 6561.
• The A. M. between two positive numbers a and b is twice the G. M. between them. Find the ratio of the numbers.
• If a, b, c, d are in G.P., then prove that 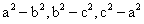 are in G.P.
• If the first and the n^th term of a G.P. are a and b, respectively, and if P is the product of n terms, prove that .
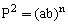• Find two positive numbers whose difference is 12 and whose AM exceeds GM by 2.
• Let ‘a’ be the AM and b & c be two GM’s between two any positive numbers. Then prove that .
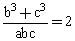• Find n such that 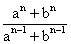 may be the G.M. between positive numbers a and b.

Queries asked on Sunday & after 7 pm from Monday to Saturday will be answered after 12 pm the next working day.