CBSE Class 11-science Maths Applications of Mathematical Induction
-
Q-6 in the image
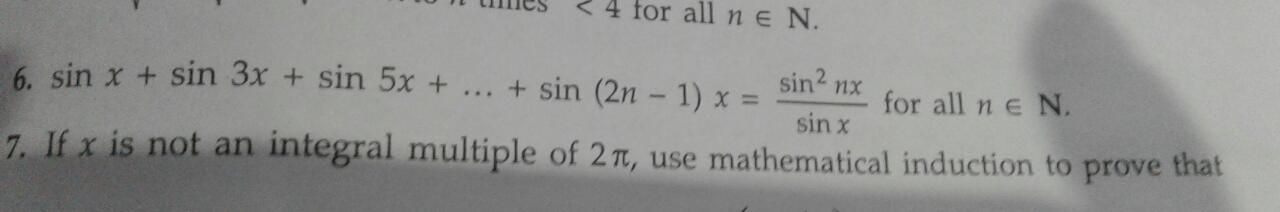
-
Prove 10th by mathatical induction
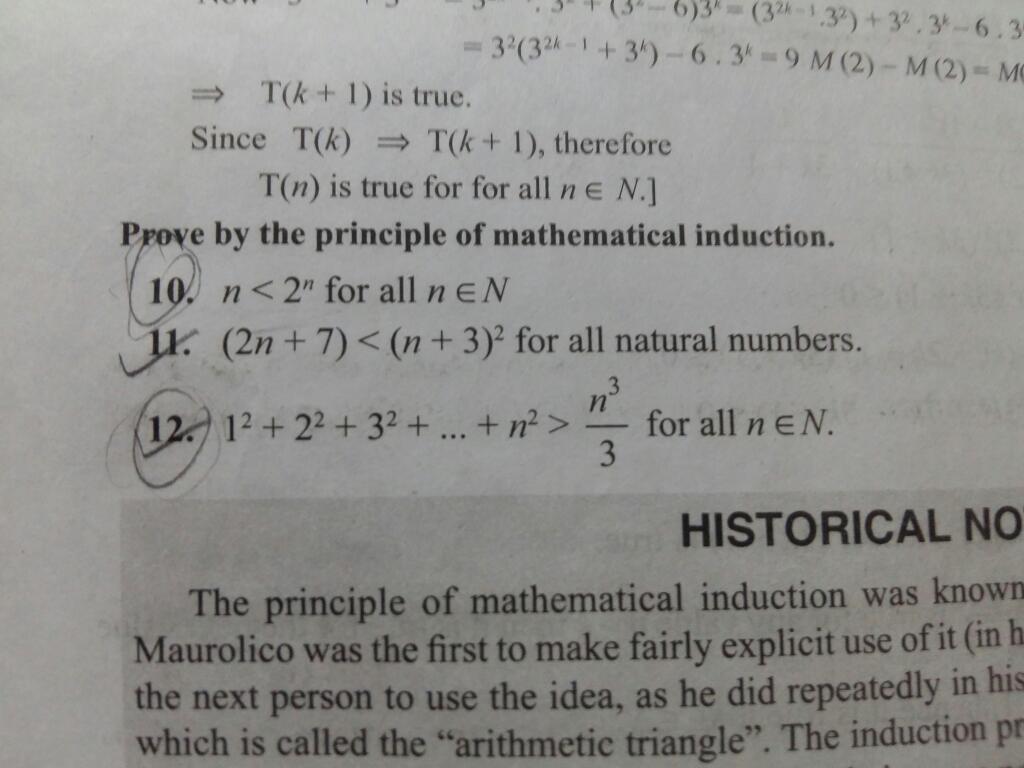
-
Prove by using the principle of mathematical induction 32n – 1 is divisible by 8 for n
 N.
N.
-
Prove by using the principle of mathematical induction n(n + 1)(n + 2) is divisible by 6 for all n
 N.
N.
- If P(n) is the statement ‘22n – 1 is multiple of 3’ then show that P(5) is true.
- Let P(n) be the statement," n3 + n is divisible by 3". Check whether P(3) and P(4) is true.
-
Prove by using the principle of mathematical induction 3n < 4n for all n
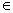 N.
N.
-
If P(n) is the statement 72n + 23n - 3.3n - 1 is divisible by 25 for all n
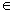 N, then what is P(k + 1)?
N, then what is P(k + 1)?
- Show that if statement P(n): 2 + 4 + 6 + --- + 2n = n( n + 1) + 2 is true for n = k, then it is also true for n = k + 1. Can we apply the principle of mathematical induction?
-
Prove that 102n – 1 + 1 is divisible by 11 for all n
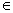 N.
N.




