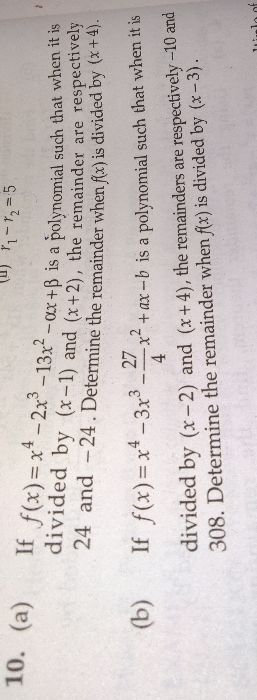CBSE Class 9 Answered
x + 6 is a factor of the polynomial mx3 + 13x2 - 69x - 18. The polynomials 3x2 - ax + 6m and x 3 + ax2 - 2 leave the same remainder when divided by (x - 2). Find the values of a and m. how to solve these type of questions
Asked by rajivjoshigoldtech | 09 Sep, 2016, 12:12: PM
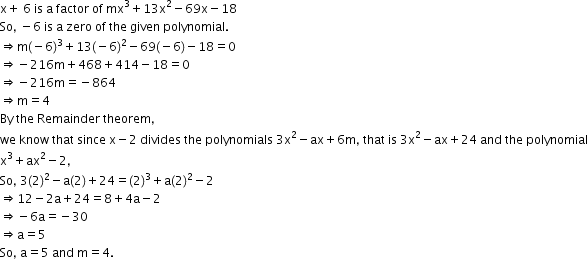
Answered by Rebecca Fernandes | 09 Sep, 2016, 12:48: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by palakbajwa21 | 24 May, 2023, 07:41: PM
CBSE 9 - Maths
Asked by 1987daljeetkaur | 22 May, 2023, 11:54: AM
CBSE 9 - Maths
Asked by shivalaxmi0205 | 21 Feb, 2023, 07:26: PM
CBSE 9 - Maths
Asked by anikk659 | 08 Jan, 2023, 03:41: PM
CBSE 9 - Maths
Asked by yeshudarsh | 05 Jul, 2022, 06:38: PM
CBSE 9 - Maths
Asked by meghapatel29121998 | 23 Jun, 2022, 10:08: PM
CBSE 9 - Maths
Asked by Chaitanyamburande | 08 May, 2022, 11:43: AM
CBSE 9 - Maths
Asked by abdulsamad82007 | 26 Jun, 2021, 02:24: PM