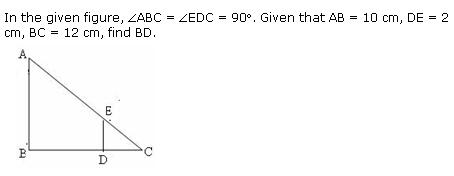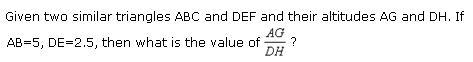CBSE Class 10 Answered

write a detailed note on congruency of triangles showing -

- types of triangles

- congruency conditions

- difference between congruent triangles and similar triangles

Asked by Mukul Kathait | 04 Jun, 2014, 11:31: PM

Expert Answer

Types of triangles:

According to the side:

If all the three sides are equal, the triangle is an Equilateral triangle.

If two sides of a triangle are equat, the triangle is an Isosceles triangle.

If all the three sides are different then it is a Scalene triangle.

According to the angle:

If all the three angles are acute, then the triangle is an acute triangle.

If one of the angles of a triangle is greater than 90, then the triangle is an Obtuse triangle.

If one of the angles in a triangle is equal to 90, then the triangle is a right triangle.

Congruency Conditions:

Two triangles are congruent if they are of the same size and shape and they are denoted by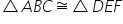

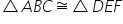
triangle A B C approximately equal to triangle D E F

Conditions for congruency:

1. SAS (Side-Angle-Side): If two pairs of sides of two triangles are equal in length, and the included angles are equal in measurement, then the triangles are congruent.

2. SSS (Side-Side-Side): If three pairs of sides of two triangles are equal in length, then the triangles are congruent.

3. ASA (Angle-Side-Angle): If two pairs of angles of two triangles are equal in measurement, and the included sides are equal in length, then the triangles are congruent.

4. AAS (Angle-Angle-Side): If two pairs of angles of two triangles are equal in measurement, and a pair of corresponding non-included sides are equal in length, then the triangles are congruent.

5. RHS (Right-angle-Hypotenuse-Side): If two right-angled triangles have their hypotenuses equal in length, and a pair of shorter sides are equal in length, then the triangles are congruent.

Similar triangles:

Similar triangles are triangles if they differ only in size.

Angles of similar triangles will be the same.

Congruent triangles are triangles with same size and angles.

Answered by Vimala Ramamurthy | 05 Jun, 2014, 12:05: PM