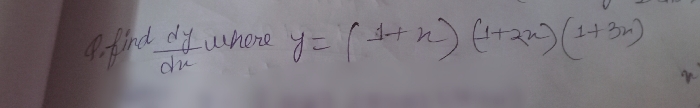CBSE Class 12-science Answered
why is g cintinous?
Asked by Rajat Somani | 21 Jul, 2011, 12:00: AM
Expert Answer
g(x+y) = g(x) g(y)
at x=0, g(0+y) = g(y) = g(0) g(y)
so g(0) = 1
If g is continuous at x=0, then g(0+y) = g(y) is continuous for all y.
Since any y can be decomposed into y=a+b, where a,b are real numbers, then g(y) = g(a) g(b) must be continuous, so g must be continuous everywhere.
If g(a) = 0 for some a in R, then write a = x+y where x,y are real numbers, then
g(a) = g(x+y) = g(x) g(y) = 0
then either g(x) = 0 or g(y) = 0 (or both).
that implies that g(x) = 0 for all x in R.
at x=0, g(0+y) = g(y) = g(0) g(y)
so g(0) = 1
If g is continuous at x=0, then g(0+y) = g(y) is continuous for all y.
Since any y can be decomposed into y=a+b, where a,b are real numbers, then g(y) = g(a) g(b) must be continuous, so g must be continuous everywhere.
If g(a) = 0 for some a in R, then write a = x+y where x,y are real numbers, then
g(a) = g(x+y) = g(x) g(y) = 0
then either g(x) = 0 or g(y) = 0 (or both).
that implies that g(x) = 0 for all x in R.
Answered by | 21 Jul, 2011, 08:06: AM
Concept Videos
-
Continuous and Discontinuous function
Understand the meaning of function to be continuous and discontinuous, comb... -
Relationship between continuity and differentiability - ...
Relationship between continuity and differentiability, concept of composite... -
Derivative of Parametric Functions
Learn the relation between two variables x and y using the third variable a... -
Second-order derivatives
Learn to find out the second-order derivatives of the given functions. -
Rolle's Theorem and its geometrical interpretation ...
Discuss Rolle's Theorem and its geometrical interpretation. Also discuss La...
CBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by fehasaf670 | 27 Jan, 2024, 01:39: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by tanyavishwakarma427 | 24 Nov, 2023, 11:56: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by sonkarmukesh007 | 13 Aug, 2023, 08:32: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by unqio66 | 15 May, 2023, 11:48: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by sdmbotch1123 | 21 Dec, 2022, 04:38: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by iasaspirant20s | 09 Oct, 2022, 02:31: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Raunaksingh4742 | 25 Aug, 2022, 12:31: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by pinkidevnict | 08 Jun, 2022, 07:51: AM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by suvajyotichaudhury998 | 04 Jun, 2022, 07:54: AM
ANSWERED BY EXPERT
