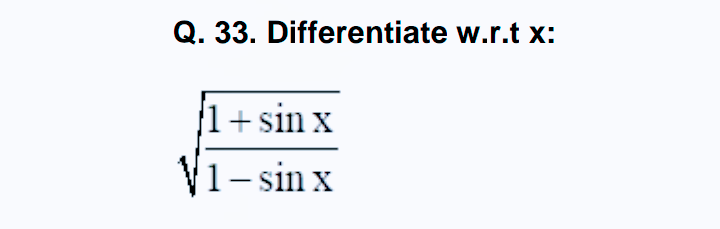CBSE Class 11-science Answered

why does when second derivative is less than zero the function is having maximum value this question which was asked by me there is no graph in it there is empty places can u resend the answer?

Asked by Gaurav Avhad | 02 May, 2011, 07:45: PM

Expert Answer

The Second Derivative Test evaluates concavity.

The Second Derivative Test tells you whether a function is concave up or concave down.

Concave Up (CU) - on an interval, the graph of the function lies above all of the tangent lines.

Concave Down (CD) on an interval, the graph of a function lies below all of the tangent lines.

If the second derivative of a function is greater than zero, for all x in an interval, the original graph is concave up.

If the derivative second of a function is less than zero, for all x in an interval, the original graph is concave down.

Points of Inflection show where a graph changes concavity.

Points of Inflection occur where the second derivative of a function equals zero or does not exist, when x is in the domain.

The Second Derivative Test states:

If the value of the critical number of the first derivative equals zero and the second derivative is greater than zero, then the original function has a local minimum at that point.

If the value of the critical number of the first derivative equals zero and the second derivative is less than zero, then the original function has a local maximum at that point.

Example: Find the points of inflection and determine the functions concavity.

f(x) = x³-3x²+x-2

Find the first derivative of the function.

f' (x) =3x²-6x+1

Find the second derivative of the function.

f'' (x) = 6x-6

= 6(x-1)

In order to determine the point of inflection set the second derivative equal to zero to isolate the x-value.

0= 6(x-1)

x=1

Substitute the x-value back into the original function to determine the order pair of the point of inflection.

f(1)=(1)³-3(1)²+(1)-2

f (1) = -3

Therefore, a point of inflection occurs at the point (1, -3).

To determine concavity, create a chart of intervals including the point of inflection x-value.

Choose a value within each interval and recognize whether the answer is negative of positive.

Negative values mean the graph is concave down on an interval.

Positive values mean the graph is concave up on an interval.

Function	Second Derivative	Conclusion
(-infinity, 1)	Negative	Concave Down
(1, infinity)	Positive	Concave Up

Therefore, concluding from the chart, from the interval (-infinity, 1) the graph is concave down and from the interval (1, infinity) the graph is concave up.

Kindly draw the graph accordingly.

Answered by | 02 May, 2011, 03:21: PM