why does rocket moves with a increasing speed?

Rocket engines produce the same force regardless of their velocity. A rocket acting on a fixed object, as in a static firing, does no useful work at all; the rocket's stored energy is entirely expended on accelerating its propellant to hypersonic speed. But when the rocket moves, its thrust acts through the distance it moves. Force acting through a distance is the definition of mechanical energy or work. So the farther the rocket and payload move during the burn, (i.e. the faster they move), the greater the kinetic energy imparted to the rocket and its payload and the less to its exhaust.

This can be easily shown. The mechanical work can be defined as

where 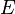 is the energy (specifically the kinetic energy),  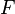is the force (the thrust of the rocket which is considered constant), and  is the distance. Differentiating with respect to time, we obtain

or

where 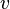 is the velocity. Dividing by the instantaneous mass  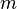to express this in terms of specific energy (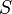), we get

where  is the acceleration vector.

Thus it can be readily seen that the rate of gain of specific energy of every part of the rocket is proportional to speed, and given this the equation can be integrated to calculate the overall increase in specific energy of the rocket.