Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

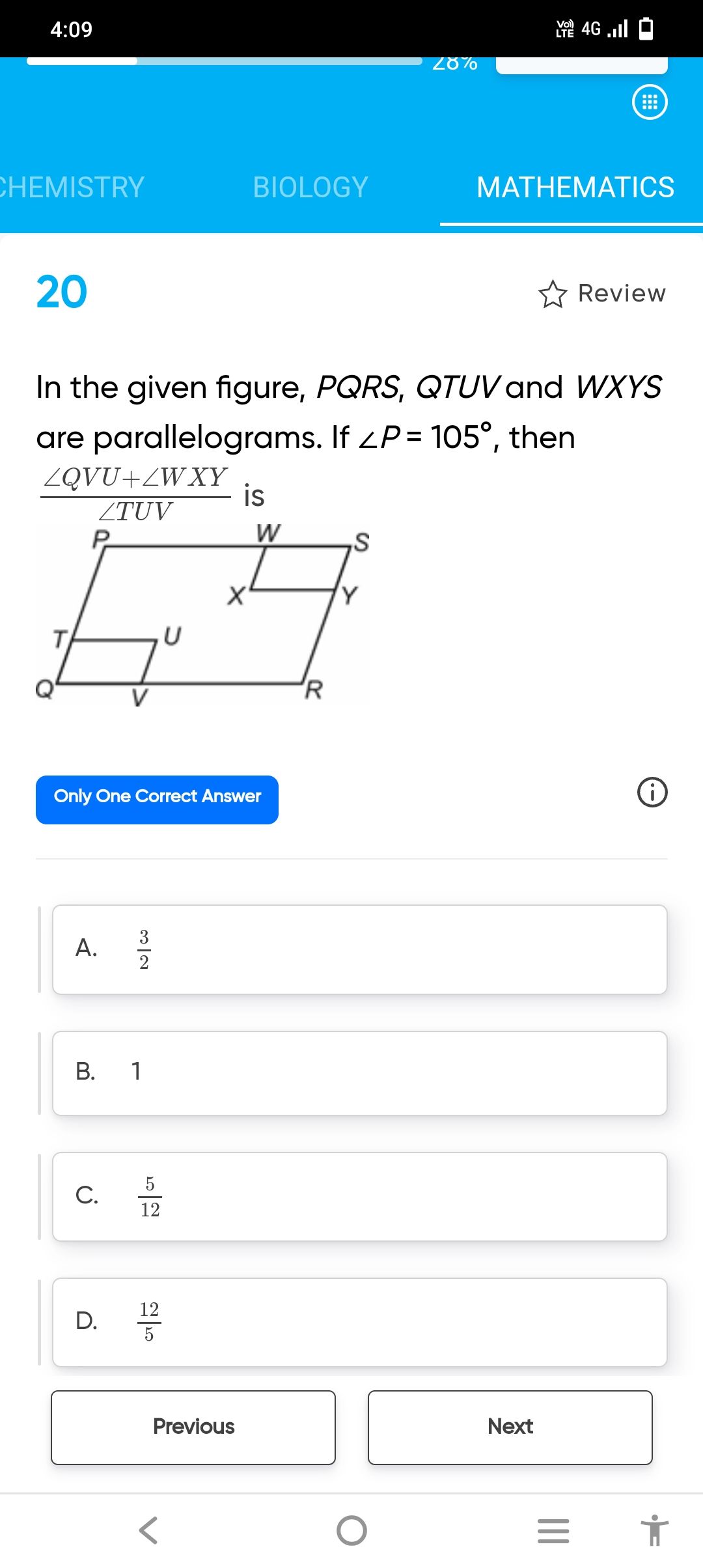
CBSE Class 9 Answered

Why concave quadrilateral do not have 360 degree as sum of all angles.
Asked by | 13 Oct, 2012, 09:12: AM
answered-by-expert Expert Answer
A special case of crossed quadrilaterals are the antiparallelograms, crossed quadrilaterals in which (like a parallelogram) each pair of nonadjacent sides has equal length. The diagonals of a crossed or concave quadrilateral do not intersect inside the shape and one angle is refler angle.
 
If you cut any quadrilateral along one of its diagonals, the figures formed are two triangles. Since the sum of the angles of a triangle is 180 degrees, then the sum of the angles of two triangles is 2(180) = 360 degrees. For this reason, the sum of the angles of a quadrilateral is 360 degrees.
Answered by | 13 Oct, 2012, 07:11: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
Prove that it in a quadrilateral each pair of opposite angles are equal them it is a paralleogram
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
If the diagonal of a parallelogram are equal,then show that it is a square.       .
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
each side of square field ABCD is 50 m long, length of diagonal field is (route 2 =1.414
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Please solve in fast
question image
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
prove that a diagonal of a parallelogram divides it into two congruent triangle
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
if the diagonal of the parrellolegram are equl then show that it is a rectangle  
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
diagonal AC of a parallelogram ABCD bisects ∆A . i . it biseets ∆C also ii . ABCD is a rhombus
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
ABCD is a Parallelogram in which ∠BAO = 35∘, ∠DAO=40∘ and ∠COD=105∘. Find ∠ABO?
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
what is ASA congruence rule
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the line segment joining the midpoints of two sides of a triangle is parallel to the third side
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×