CBSE Class 9 Answered
what is the ratio of the area of a square inscribed in a semi circle to the area inscribed in a quadrant of the same circle
Asked by | 22 Oct, 2012, 11:28: AM
Expert Answer
In a semicircle of radius r, an inscribed square will touch the circumference at two points symmetrically placed about the centre of the base. Drawing the radius to one of these points will produce a triangle with base s/2 and height s, where s is the length of the sides of the square. By Pythagoras we have r² = s² + (s/2)² = (5/4)s² and hence the area of the square s² = (4/5)r²
In a quadrant of a circle with centre O, the inscribed square has one corner at O and sides of equal lengths s such that the diagonally opposite corner touches the circumference at point A. Applying Pythagoras to the radius OA gives s² + s² = r², so that the area of this square is s² = r²/2.
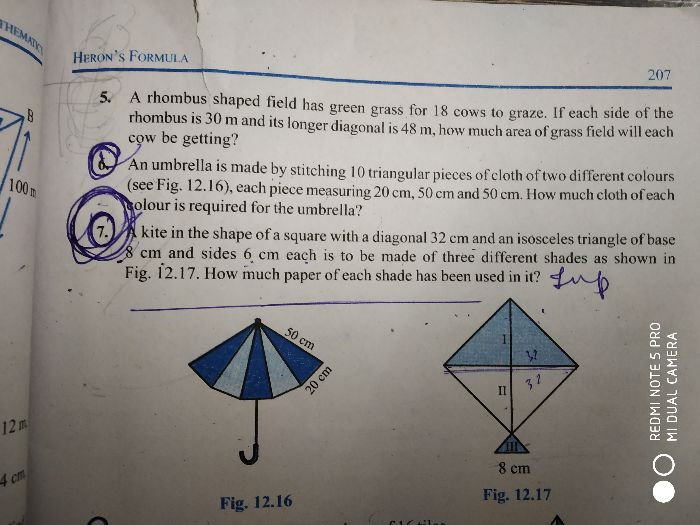
Hence the ratio of the area of the square inscribed in a semicircle to that inscribed in a quadrant of the same radius is (4/5)/(1/2) = 8/5 that is, last option.
In a quadrant of a circle with centre O, the inscribed square has one corner at O and sides of equal lengths s such that the diagonally opposite corner touches the circumference at point A. Applying Pythagoras to the radius OA gives s² + s² = r², so that the area of this square is s² = r²/2.
Hence the ratio of the area of the square inscribed in a semicircle to that inscribed in a quadrant of the same radius is (4/5)/(1/2) = 8/5 that is, last option.
Answered by | 23 Oct, 2012, 12:02: AM
Application Videos
-
Application of Heron's Formula - 1
This video explains an application of Heron's Formula. -
Problem on Heron's Formula - 1
This video explains an application of Heron's Formula. -
Problem on Heron's Formula - 2
This video explains an application of Heron's Formula.
-
Application of Heron's Formula - 2
This video explains an application of Heron's Formula.
Concept Videos
-
Concepts and problem solving based on Heron's formula ...
Introduction to Heron's formula and using the formula to find the area of s... -
Application of Heron's Formula
This video explains the derivation of the Heron's formula for the area of t... -
Heron's Formula concepts
Introduction to Heron's formula and using the formula to find the area of s... -
Heron's formula - derivation and problem-solving
Derivation of the Heron's formula for the area of triangle.. It's applicati... -
Heron's Formula: Exam Prep Strategies
Introduction to Heron's formula and using the formula to find the area of s...
CBSE 9 - Maths
Asked by seemarajpoot01101986 | 29 Nov, 2023, 04:40: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by shrikantsalunkhe1012 | 10 Jun, 2023, 06:47: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by vasumathir1978 | 25 Aug, 2021, 11:08: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by saanvichhikara07 | 23 Sep, 2020, 08:10: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by kynarahman | 20 Aug, 2020, 07:53: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by arumugaperumalr17 | 09 Aug, 2020, 10:00: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by gauravbhardwaj65950 | 25 Apr, 2020, 09:45: PM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by kirtisatpute995 | 14 Feb, 2020, 11:22: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by kirtisatpute995 | 14 Feb, 2020, 11:21: AM
ANSWERED BY EXPERTCBSE 9 - Maths
Asked by karanbora625 | 29 Oct, 2019, 12:16: PM
ANSWERED BY EXPERT
