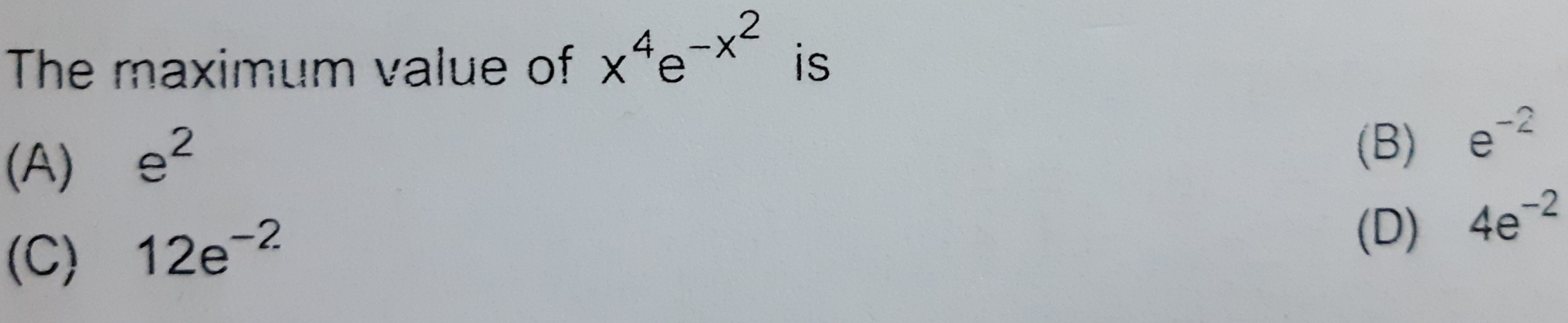Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

What is the difference between finding the local maxima/minima and absolute maxima/minima of a differential equation?
Asked by Susan fletcher | 18 Feb, 2014, 11:56: AM
answered-by-expert Expert Answer
The maximum and minimum of a function, are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain.
 
A function f has a local minimum at x=a if f open parentheses x close parentheses greater or equal than f open parentheses a close parentheses near r
Similarly, a function f has a local maximum at x=a if f open parentheses x close parentheses less or equal than f open parentheses a close parentheses near a.
A function f has a global minimum at x=a if f open parentheses x close parentheses greater or equal than f open parentheses a close parentheses all over the domain.
Similarly, a function f has a global maximum at x=a if f open parentheses x close parentheses less or equal than f open parentheses a close parentheses all over the domain.
Let us observe the following figure.
 
Answered by | 18 Feb, 2014, 12:53: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
Find the local maxima and local minima for the given function and also find the local maximum and local minimum values f(x)=x99, xf(-3,3)
Asked by srisrinivasa.mcrl | 04 Feb, 2024, 10:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
solve this aod question
question image
Asked by shubh31122006 | 23 Dec, 2023, 02:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
ex 6.5 maths q 3 - vii
Asked by lailavafra08 | 26 Oct, 2023, 07:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
pls provide solution
question image
Asked by saisidh05 | 04 Jul, 2022, 03:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the angle of  intersection of 2 curve x^2y=2 and xy^2=4    
Asked by agarwalgolu318 | 13 Aug, 2020, 08:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5m/s. When the base of the ladder is 8 metres from the wall, i) How fast is the top of the ladder moving down the wall? ii) At what rate, the area of the triangle formed by the ladder, wall, and the floor, is changing ?
Asked by jeevasankar123456 | 17 Jul, 2020, 05:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Differentiate Sin x
Asked by givduf | 11 Jul, 2020, 09:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
the height of a right circular cone is 24 cm whose curved surface area is 550 cm square .find it's volume
Asked by clbalaji.cnhalli | 05 Feb, 2020, 08:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Fimd the point of local maxima and local minima and corresponding local maxima and local minima values of each of the following funct. F(x) = x^3 -2ax^2 a^2x, a>0 ,x belongs to real no.
Asked by Ronitupadhyay13 | 20 Dec, 2019, 12:28: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
What will be the answer for this question?
question image
Asked by dineshchem108 | 09 Oct, 2019, 07:04: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×