Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

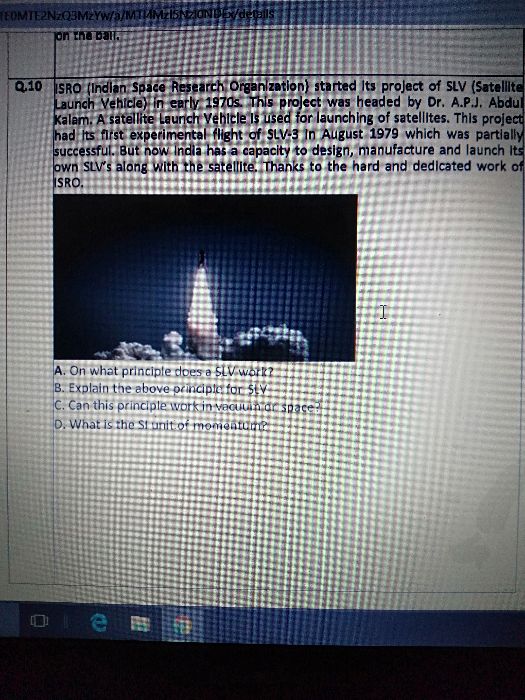
CBSE Class 9 Answered

what is the basic concept of coservation of momentum?
Asked by Akshya Achu | 21 Aug, 2014, 08:13: PM
answered-by-expert Expert Answer
According to the second law of motion we know that moving bodies possess momentum and is equal to the product of mass and velocity.
                                    p = m v
According to the law of conservation of momentum " When two or more bodies act upon one another, their total momentum remains constant provided no external force are acting."
Consider a collision between a moving and a stationary object. When the collision occurs, the velocity of the moving object decreases, but at the same time, the velocity of the stationary object increases.Due to this the momentum of moving object decreses and the momentum of the stationary object increases.The increase in the momentum of the stationary object is equal to the decrease in the momentum of the moving object.Thus there is no loss of momentum during collision.
Thus, the law of conservation of momentum can be stated as the sum of momenta of objects before collision is equal to the sum of momenta after collision, provided there is no external force acting on the objects.
 
Consider two objects A and B of masses mA and mB initially moving in a straight line with velocities uA and uB, respectively. Assume that uA > uB. They collide with each other as shown below. The total momentum of the two objects before collision is mAuA+mBuB.

 

 

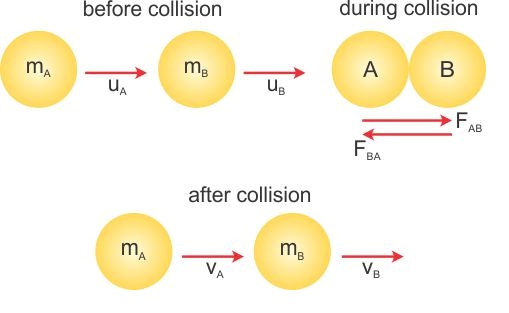
 The collision lasts for time t. During this collision, A exerts a force FAB on B and B exerts a force FBA on A.Suppose vA and vB are the velocities of A and B after collision, the momentum before and after collision for object A is mAuA and mAvA respectively. Thus, according to Newton's law, the force FAB  can be written as :

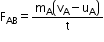
                              Syntax error from line 1 column 49 to line 1 column 73. Unexpected '<mstyle '.

 Similarly, the force FBA on A is:

                             Syntax error from line 1 column 49 to line 1 column 73. Unexpected '<mstyle '.

According to the third law of motion, we have :

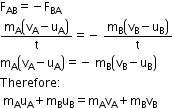
Syntax error from line 1 column 49 to line 1 column 73. Unexpected '<mstyle '.

 i.e The total momentum of both objects A and B before collision is equal to the total momentum of both objects after collision.

Thus, the momentum is conserved in a collision.

Answered by Jyothi Nair | 22 Aug, 2014, 09:18: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Physics
A boy of mass 45 kg running 6 m/s jumps onto a 30 kg trolley moving in the same direction at 1.5 m/s. Their common velocity will be: A. 4.0 m/s B. 4.2 m/s C. 6.5 m/s D. 8.3 m/  
Asked by nishitatrambadia | 21 Oct, 2021, 09:38: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
what is linear momentum ?
Asked by frusbJusyktsnis | 17 Sep, 2021, 12:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
a bullet of mass 20 grams is horizontally fired with a volicity of 150 mls from pistal of mass 2 kg what is the recoil volicity of pistal
Asked by gaminggaming64738 | 28 Jun, 2021, 10:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
Two hockey players of opposite teams, while trying to hit a hockey ball on the ground collide and immediately become entangled. One has a mass of 60 kg and was moving with a velocity 5.0 m s–1 while the other has a mass of 55 kg and was moving faster with a velocity 6.0 m s–1 towards the first player. In which direction and with what velocity will they move after they become entangled? Assume that the frictional force acting between the feet of the two players and ground is negligible.
Asked by sasikumarsarala2020 | 25 Jun, 2021, 04:37: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
vehicle stops on applying brakes does this phenomena violate the principle of conservation of momentum momentum momentum
question image
Asked by neeteshvarshney6 | 20 Jul, 2020, 04:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
please answer fast
question image
Asked by tapandash1974 | 16 Jul, 2020, 05:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
question number 33
question image
Asked by neha14072006 | 21 Jun, 2020, 08:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
A bullet of mass 3 kg is fired with a velocity of 150 metre per second find its momentum  
Asked by pnegi9416 | 29 Apr, 2020, 10:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
A ball moving at a constant speed 10m/s, hits normally on a wall (mass of ball is 50g) and rebounds with same speed. The change in momentum is
Asked by mohitdhoni706 | 03 Apr, 2020, 01:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Physics
The mass of a cannon is 500 kg.  From this cannon a bullet of 10 kg mass was thrown at a speed of 20 m / s.  How long does a cannon retreat if the resistance of the land is one tenth the weight of the cannon?
Asked by asishsengupta51 | 20 Feb, 2020, 11:24: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×