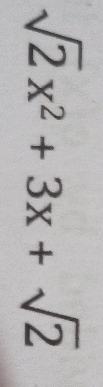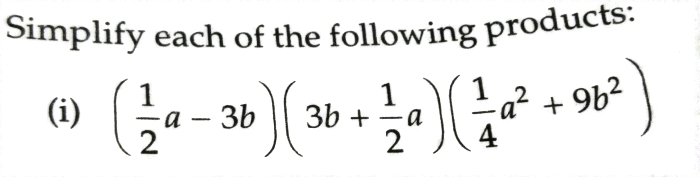CBSE Class 9 Answered
what is exactly remainder theorm?
Asked by Raveesha Chaubey | 07 Jun, 2013, 10:52: AM
REMAINDER THEOREM
if P(x) is a polynomial in x then the remainder on dividing P(x) by x ? a is P(a)
PROOF:
Let q(x) be the quotient and r(x) be the remainder obtained when the polynomial p(x) is divided by (xa).
Then, p(x) = (xa) q(x) + r(x), where r(x) = 0 or some constant.
Let r(x) = c, where c is some constant. Then
p(x) = (xa) q(x) + c
Putting x = a in p(x) = (xa) q(x) + c, we get
p(a) = (aa) q(a) + c
? p(a) = 0 x q(a) + c
? p(a) = c
This shows that the remainder is p(a) when p(x) is divided by (xa).
Answered by | 08 Jun, 2013, 12:47: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by durgavenkatlakshmi1 | 20 Mar, 2024, 03:56: PM
CBSE 9 - Maths
Asked by ammudeep0123 | 20 Mar, 2024, 07:13: AM
CBSE 9 - Maths
Asked by jaswanthsompi12345 | 19 Dec, 2023, 06:54: PM
CBSE 9 - Maths
Asked by rizwanmunna406 | 12 Dec, 2023, 10:09: PM
CBSE 9 - Maths
Asked by sathishdoddamudigere2 | 01 Nov, 2023, 06:53: PM
CBSE 9 - Maths
Asked by shambhushanker123 | 29 Oct, 2023, 08:36: PM