CBSE Class 10 Answered
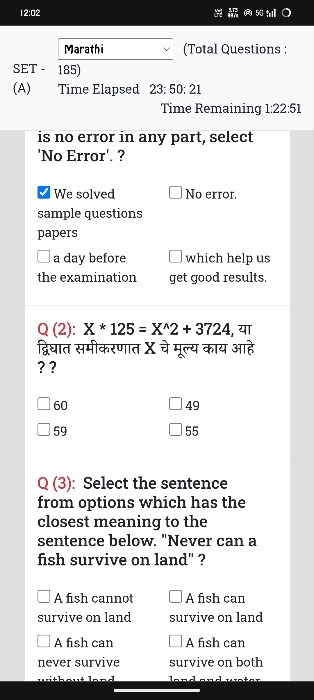
Water flows at the rate of 10 metre per second through a cylindrical pipe having its diameter as 5 mm. How much time will it take to fill a conical vessel whose diameter of base is 40 cm and depth 24 cm?
Asked by | 26 Jan, 2014, 07:11: AM
Radius of the pipe = 5/2 mm = (5/2) x (1/10) = 1/4 cm
Speed of water = 10 x 100 cm/sec = 1000cm/sec
Volume of water that flows in 1 second = ? r^2 h = 22/7 x 1/4 x 1/4 x 1000 = 1375/7 cm^3
Radius of conical vessel = 40/2 = 20 cm; Depth = 24 cm
Therefore, Capacity of the vessel = 1/3 x ? r^2 h
= 1/3 x 22/7 x 20 x 20 x 24 = 70400/7 cm^3
Therefore, Time required to fill the vessel = capacity of the vessel / volume of water flowing per second
=(70400/7) / (1375/7) = 70400/1375 = 256/5 seconds = 51 .2 sec
Answered by | 29 Jan, 2014, 04:38: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
CBSE 10 - Maths
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
CBSE 10 - Maths
Asked by mustafahssn786 | 23 Mar, 2024, 06:25: AM
CBSE 10 - Maths
Asked by choudharyniki001 | 22 Mar, 2024, 08:49: AM
CBSE 10 - Maths
Asked by jagdishdabang79 | 18 Mar, 2024, 08:40: PM