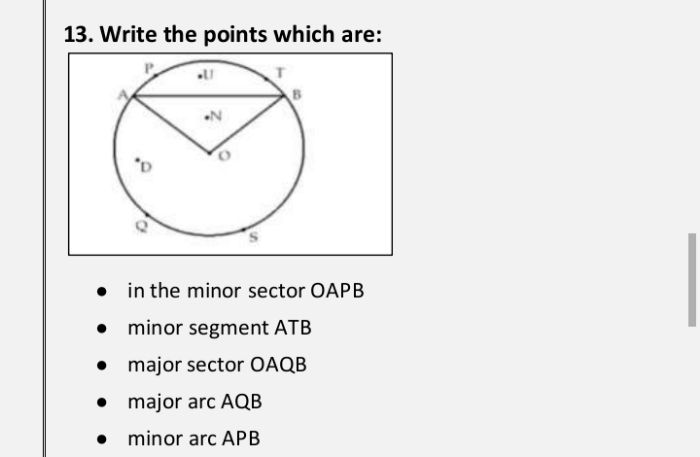
CBSE Class 9 Answered

Given: Two circles with centre A and B intersect each other at point P and Q.

            PQ is the common chord to the circles.

To Prove:  AB is the perpendicular bisector of a common chord

Proof: We know that the line from the centre is perpendicular bisector of the chord.

The line BL passing from centre B, BLP = 90^o .................(1)

PL = PQ.  ......................(2)

The line AL passing from centre A, ALP = 90^o .............(3)

Now, BLP +  ALP  = 180^o                (From (1) and (3))

i.e AB is staright line with L as a point on it.

From (1), (2) and (3)

The line AB is a perpendicular bisector of the common chord PQ