CBSE Class 12-science Answered
Verify Rolle’s theorem for the function f (x) = (x – a)m (x – b)n on the interval [a, b], where m, n are positive integers.
Asked by Topperlearning User | 05 Aug, 2014, 08:38: AM
We have, f (x) = (x – a)m (x – b)n where m, n Î N
On expanding (x – a)m and (x – b)n by binomial theorem and then taking the product, we find that f (x) is a polynomial of degree (m + n). Since a polynomial function is everywhere differentiable and so continuous also. Therefore,
(i) f (x) is continuous on [a, b]
(ii) f (x) is derivable on (a, b)
Also, f (a) = f (b) = 0
Thus, all the three conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c Î (a,b) such that f ¢ (c) = 0
We have,
f (x) = (x – a)m (x – b)n
Þ f ¢ (x) = m (x – a)m – 1 (x – b)n + (x – a)m n (x – b)n – 1
Þ f ¢ (x) = (x – a)m – 1 (x – b)n – 1 {m (x – b) + n (x – a)}
Þ f ¢ (x) = (x – a)m – 1 (x – b)n – 1 {x (m + n) – (mb + na)}
\ f ¢ (x) = 0
Þ (x – a)m – 1 (x – b)n – 1{x (m + n) – (mb + na)} = 0
Þ (x – a) = 0 or (x – b) = 0 or x (m + n) – (mb + na) = 0
Þ x = a or, x = b or, x = 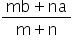
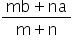
Since x = 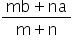 divides (a, b) into the ratio m : n. Therefore,
divides (a, b) into the ratio m : n. Therefore, 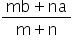 Î (a, b).
Î (a, b).
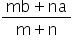 divides (a, b) into the ratio m : n. Therefore,
divides (a, b) into the ratio m : n. Therefore, 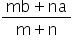 Î (a, b).
Î (a, b).Thus, c = 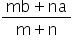 Î (a, b) such that f ¢ (c) = 0
Î (a, b) such that f ¢ (c) = 0
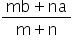 Î (a, b) such that f ¢ (c) = 0
Î (a, b) such that f ¢ (c) = 0Hence, Rolle’s theorem is verified.
Answered by | 05 Aug, 2014, 10:38: AM
Concept Videos
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 03:57: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 04:00: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 04:03: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 04:11: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 05 Aug, 2014, 08:38: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 03:32: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 03:48: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 04:16: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Aug, 2014, 04:35: PM





 on [– 2, 2].
on [– 2, 2]. on [a, b], where 0 < a < b.
on [a, b], where 0 < a < b.
