Verify Rolle’s theorem for each of the following functions on indicated intervals :
f(x) = sin x + cos x – on 
Asked by Topperlearning User
| 4th Aug, 2014,
04:16: PM
Expert Answer:
Since sin x and cos x are everywhere continuous and differentiable. Therefore, f (x) = sin x + cos x – 1 is continuous on 
and differentiable on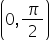 
Also, f (0) = sin 0 + cos 0 – 1 = 0 and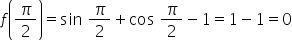 
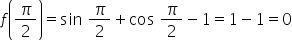
\ f (0) =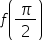 
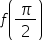
Thus, f (x) satisfied conditions of Rolle’s theorem on Therefore, there exists c ε 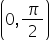such that f ¢ (c) = 0
Therefore, there exists c ε 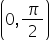such that f ¢ (c) = 0Þ cos x – sin x = 0 Þ sin x = cos x Þ tan x = 1 Þ x = 
Thus, c =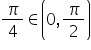 
such that f ¢ (c) = 0
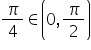such that f ¢ (c) = 0Hence, Rolle’s theorem is verified
Answered by
| 4th Aug, 2014,
06:16: PM
Concept Videos
- Discuss the applicability of Rolle’s theorem for the following function on the indicated interval: f(x) = |x| on [–1, 1]
- Discuss the applicability of Rolle’s theorem for the following function on the indicated interval : f (x) = 3 + (x – 2)2/3 on [1, 3]
- Discuss the applicability of Rolle’s theorem for the following function on the indicated interval: f (x) = tan x on [0, p]
- Discuss the applicability of Rolle’s theorem on the function f (x) =
- Verify Rolle’s theorem for the function f (x) = x2 – 5x + 6 on the interval [2, 3].
- Verify Rolle’s theorem for the function f (x) = (x – a)m (x – b)n on the interval [a, b], where m, n are positive integers.
- Verify Rolle’s theorem for the function f (x) =
on [– 2, 2].
- Verify Rolle's theorem for the function f (x) =
on [a, b], where 0 < a < b.
- Verify Rolle's theorem for each of the following functions on indicated intervals : f (x) = sin x – sin 2 x on [0, p]
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change