CBSE Class 8 Answered
Using Euler's formula, find the unknown.
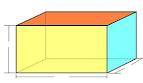
(i)
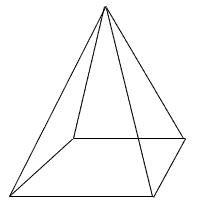
(ii)
Faces
x
5
Vertices
6
y
Edges
12
9
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
Expert Answer
Euler's Formula: F + V - E = 2
Case(i) Here, F = x, V = 6 and E = 12
Therefore, F + V - E = 2
Or, x + 6 - 12 = 2
Or, x - 6 = 2
Or, x = 2 + 6 = 8
Hence, number of faces are 8.
Case (ii) Here, F = 5, V = y and E = 9
Therefore, F + V - E = 2
Or, 5 + y - 9 = 2
Or, y - 4 = 2
Or, y = 2 + 4 = 6
Hence, number of vertices are 6.
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 8 - Maths
Asked by praveenpk5903 | 31 Dec, 2019, 05:14: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 13 Dec, 2013, 10:57: AM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 29 Nov, 2013, 12:53: AM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERTCBSE 8 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT
