Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Two protons separated by a distance 'r' travelling n the same direction with velocity 'v' show that the ratio of magnetic and electric forces acting between them is (v/c)^2, c is the speed of light.
Asked by Tanya raj | 21 Aug, 2015, 08:19: PM
answered-by-expert Expert Answer
The electric force between the two protons is given as
 
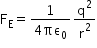
begin mathsize 14px style straight F subscript straight E equals fraction numerator 1 over denominator 4 πε subscript 0 end fraction straight q squared over straight r squared end style
Now, the magnetic force is given as FB = qvB
 
To find B:
 
The magnetic field is given from Biot-Savarts law as
 
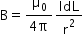
begin mathsize 14px style straight B equals fraction numerator straight mu subscript 0 over denominator 4 straight pi end fraction IdL over straight r squared end style
dL is the length element of the conductor. However, we do not have any conductor here, but only protons moving.
 
So, the expression will be altered for charge and not current.
 
We know that I = q/t, so in time dt, the current moves a length dL. So, we get
 
I dL = q dL/dt = qv
 
Hence, the magnetic field is
 
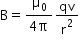
begin mathsize 14px style straight B equals fraction numerator straight mu subscript 0 over denominator 4 straight pi end fraction qv over straight r squared end style
 
Therefore, the magnetic force is given as
 
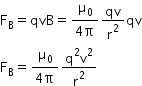
begin mathsize 14px style straight F subscript straight B equals qvB equals fraction numerator straight mu subscript 0 over denominator 4 straight pi end fraction qv over straight r squared qv straight F subscript straight B equals fraction numerator straight mu subscript 0 over denominator 4 straight pi end fraction fraction numerator straight q squared straight v squared over denominator straight r squared end fraction end style
 
Hence, the ratio of electric and magnetic forces is
 
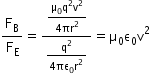
begin mathsize 14px style straight F subscript straight B over straight F subscript straight E equals fraction numerator fraction numerator straight mu subscript 0 straight q squared straight v squared over denominator 4 πr squared end fraction over denominator fraction numerator straight q squared over denominator 4 πε subscript 0 straight r squared end fraction end fraction equals straight mu subscript 0 straight epsilon subscript 0 straight v squared end style
 
Now, we know that the speed of light is given as
 
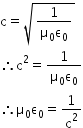
begin mathsize 14px style straight c equals square root of fraction numerator 1 over denominator straight mu subscript 0 straight epsilon subscript 0 end fraction end root therefore straight c squared equals fraction numerator 1 over denominator straight mu subscript 0 straight epsilon subscript 0 end fraction therefore straight mu subscript 0 straight epsilon subscript 0 equals 1 over straight c squared end style
 
Therefore, we get the ratio as
 
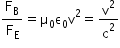
begin mathsize 14px style straight F subscript straight B over straight F subscript straight E equals straight mu subscript 0 straight epsilon subscript 0 straight v squared equals straight v squared over straight c squared end style
Answered by Romal Bhansali | 22 Aug, 2015, 09:05: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
An electron moves in a circular orbit of radius 0.51A around a nucleus at a frequency of 6.8times10^(15)Hz .Estimate the magnetic field at the nucleus
Asked by bogarpradnya | 03 Mar, 2020, 08:42: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
how are the magnetic field lines different from the electrostatic field lines.
Asked by 101206077443105 | 02 Sep, 2018, 08:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Why cyclotron can not be used to accelerate neutron?
Asked by Topperlearning User | 08 May, 2015, 10:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Why cyclotron is not suitable for accelerating electrons?
Asked by Topperlearning User | 08 May, 2015, 10:31: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Write any two uses of cyclotron.
Asked by Topperlearning User | 08 May, 2015, 10:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Why the set up of cyclotron is placed in an evacuated chamber?
Asked by Topperlearning User | 08 May, 2015, 10:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
An electron beam was deflected in a given field which was perpendicular to the beam. The beam follows a parabolic path after deflection. Give answer whether the field was electric field or magnetic field.
Asked by Topperlearning User | 08 May, 2015, 10:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
What will be the force on a charged particle moving in a region where uniform electric as well as magnetic field are acting?
Asked by Topperlearning User | 18 May, 2015, 11:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
What do you mean by cyclotron frequency?
Asked by Topperlearning User | 08 May, 2015, 10:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Derive an expression for maximum energy gained by the positive ion using a cyclotron.
Asked by Topperlearning User | 08 May, 2015, 10:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×