Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Two equal small spheres each weighing 1g , hang by two equal silk threads from the same point. The spheres are charged when in contact and come to rest with their centres 2cm apart and 20cm vertically below the point of support. Find the charge on each sphere. 
Asked by ishantkundu31 | 14 Jun, 2021, 05:00: PM
answered-by-expert Expert Answer
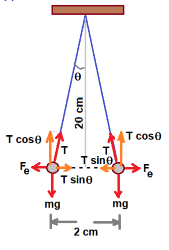
Figure shows forces acting on charged sphere. Weight mg is acting downward.  Repulsive electrostatic force is shown as Fe .
 
Tension force T acting along string is resolved as ( T cosθ ) and ( T sinθ ) . 

(Tcosθ) component balances weight mg.   (T sinθ) component balances Electrostatic force Fe . 
 
T cosθ = mg ...................... (1)

T sinθ  = Fe ........................(2)
 
If we eliminate tension T in above equations, we get ,  Fe = m g tanθ .......................(3)
 
Eqn.(3) is written as
 
K × ( q2 / d2 ) = ( m g tanθ ) ........................... (4)
 
where K = 1/( 4 π εo ) = 9 × 109 N m2 C-2 Coulomb's constant  and d = 2 cm  is the distance between charged spheres.
 
m is mass of sphere , g is acceleration due to gravity and θ is the angle made by the string with vertical
 
From eqn.(4) , we get 
 
begin mathsize 14px style q space equals space square root of open parentheses fraction numerator m space g space tan theta space d squared over denominator K end fraction close parentheses end root space space end style
 
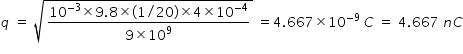
begin mathsize 14px style q space equals space square root of fraction numerator 10 to the power of negative 3 end exponent cross times 9.8 cross times left parenthesis 1 divided by 20 right parenthesis cross times 4 cross times 10 to the power of negative 4 end exponent over denominator 9 cross times 10 to the power of 9 end fraction end root space equals 4.667 cross times 10 to the power of negative 9 space end exponent C space equals space 4.667 space n C end style
Answered by Thiyagarajan K | 14 Jun, 2021, 09:41: PM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Physics
calculate the distance between two protons if the repulsive force acting between them is equal to weight a proton
Asked by rishabhverma895334 | 01 Mar, 2024, 07:24: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
electric charges
question image
Asked by rameshsanju123 | 08 Feb, 2024, 08:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
explain coulambs law give unit and dimensions of electrostatics constant and coulambs law in vector form with superposition principle
question image
Asked by bhatig9772 | 09 Jan, 2023, 06:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
calculate column b force between alpha particles separated by a distance of 3.2 into 10 to the power minus 15 m in air
Asked by bhagawan5225 | 06 May, 2022, 05:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Two similar spheres having +Q and -Q charges at a kept distance . F force act on between two.if at the middle of the two sphere another similar sphere having +Q is kept then it experience a force in magnitude and direction as
Asked by nonuhasan2 | 28 Nov, 2021, 09:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
what is dielectric current
Asked by komalshakatawat18 | 19 Sep, 2021, 05:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
There is one charged tiny spherical oil drop and the magnitude of electric field intensity at a point on its surface is E. If n such drops are combined to make a single drop then what will be the net electric field intensity at a point on the surface of the bigger spherical drop. Assume that charge is uniformly distributed over the volume of oil drop.
Asked by jangraarti2 | 31 Jul, 2021, 07:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
the force between two charges at distance r is f what will be the force between these charges if the distance between them is doubled and charges are placed in a medium of dielectric constant 10 ?
Asked by aditya.loya9821 | 23 Jul, 2021, 06:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
A point charge qa = + 100 c is placed at point a (1, 0, 2) m and another point charge qb = +200c isplaced at point b (4, 4, 2) m. Find :(i) magnitude of electrostatic interaction force acting between them(ii) find a f(force on a due to
Asked by raghavsumit9690 | 10 Jul, 2021, 01:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Physics
Two identical metal spheres have charges +15μC and +25μC areseparated by a distance. If the spheres are first brought into contact and then separated to the original distance, then the ratio of the new force to the previous force is 
Asked by mohammedmuhsin786786 | 01 Jul, 2021, 08:33: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×