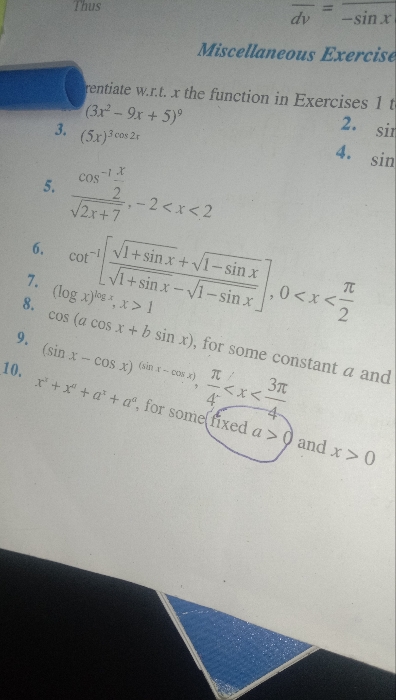CBSE Class 12-science Answered
to prove:-
Asked by | 20 Feb, 2009, 05:13: PM
Beginning with the ubiquitous triple product identity
Ax(BxC) = B(A.C)-C(A.B) (1)
for vectors in R^3, we immediately have the handy formula for the
cross product of two cross products
(AxB)x(CxD) = B[(CxD).A] - A[(CxD).B]
Answered by | 22 Feb, 2009, 02:32: PM
Application Videos
Concept Videos
CBSE 12-science - Maths
Asked by aishaazmata | 24 Apr, 2024, 08:48: PM
CBSE 12-science - Maths
Asked by revengesena | 24 Apr, 2024, 06:08: PM
CBSE 12-science - Maths
Asked by mahammadsharifdakhani67 | 16 Apr, 2024, 07:43: PM
CBSE 12-science - Maths
Asked by 20muskaansharma23 | 08 Apr, 2024, 11:31: AM
CBSE 12-science - Maths
Asked by cherrycharishma512 | 01 Apr, 2024, 12:32: PM
CBSE 12-science - Maths
Asked by annapoornaa429 | 31 Mar, 2024, 08:23: PM
CBSE 12-science - Maths
Asked by shirishakuruva477 | 28 Mar, 2024, 09:52: PM
CBSE 12-science - Maths
Asked by sheensvlog | 27 Mar, 2024, 10:15: PM