CBSE Class 11-science Answered
The speed of a particle of mass m, moving in a circle of radius r, is changing at a constant rate aT m/ s2. Write the expression for the magnitude of its instantaneous resultant acceleration. Can we say that the direction of this instantaneous resultant acceleration would be along the instantaneous (inward) radial acceleration
Asked by pranayshah1908 | 28 Feb, 2021, 12:18: PM
If speed of particle moving in a circular path is chanigin at a constant rate aT , then tangential acceleration = aT
Speed of particle v by assuming speed is 0 at t = 0 is given as
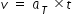
Radial acceleration, aR = v2 / R
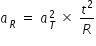
where R is radius of circular path
Resultant instantaneous acceleration a = 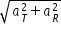
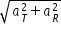
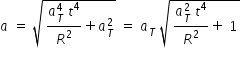
Instantaneous acceleration is not along the direction of radial accleration because radial acceleration and
tangential acceleration are perpendicular to each other.
Answered by Thiyagarajan K | 28 Feb, 2021, 03:04: PM
CBSE 11-science - Physics
Asked by sheikhsaadat24 | 17 Apr, 2024, 09:41: PM
CBSE 11-science - Physics
Asked by sy123946 | 07 Apr, 2024, 04:23: PM
CBSE 11-science - Physics
Asked by derhebha955 | 03 Apr, 2024, 09:03: AM
CBSE 11-science - Physics
Asked by sumedhasingh238 | 29 Mar, 2024, 05:15: PM
CBSE 11-science - Physics
Asked by sumedhasingh238 | 28 Mar, 2024, 11:10: PM
CBSE 11-science - Physics
Asked by roshnibudhrani88 | 23 Mar, 2024, 05:52: PM
CBSE 11-science - Physics
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by om636694 | 04 Mar, 2024, 09:10: PM
CBSE 11-science - Physics
Asked by rajuinwati12 | 04 Mar, 2024, 09:22: AM




