CBSE Class 12-science Answered
The space s described in time t by a particle moving in a straight line is given by s=t^5-40t^3+30t^2+80t-250. Find the minimum value of its acceleration.
Asked by shaktidevgun | 28 May, 2016, 07:10: PM

Answered by satyajit samal | 29 May, 2016, 05:39: PM
Concept Videos
CBSE 12-science - Maths
Asked by srisrinivasa.mcrl | 04 Feb, 2024, 10:39: AM
CBSE 12-science - Maths
Asked by Ronitupadhyay13 | 20 Dec, 2019, 12:28: AM
CBSE 12-science - Maths
Asked by tv2000in | 28 May, 2019, 12:02: AM
CBSE 12-science - Maths
Asked by Kchawla94 | 02 Apr, 2019, 06:45: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 21 Aug, 2014, 01:22: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:25: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 21 Aug, 2014, 12:21: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 08:45: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:38: AM




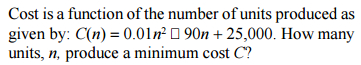

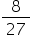 of the volume of the sphere.
of the volume of the sphere.