CBSE Class 9 Answered
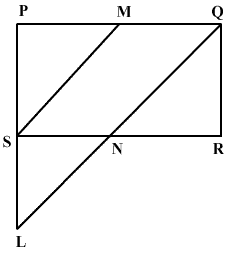
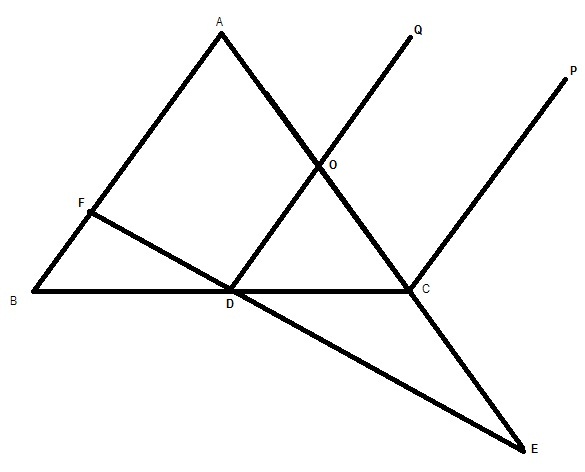
The side AC of a triangle ABC is produced to E such that CE = 1/2 AC. If D is midpoint of BC and ED produced meets AB in F, and CP, DQ are drawn parallel to BA. Prove that FD = 1/3 EF
Asked by Paresh | 08 Dec, 2015, 04:26: PM

Answered by Vijaykumar Wani | 09 Dec, 2015, 11:32: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:58: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 12:01: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:52: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:56: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM