Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

The set of real number x for which x2-|x+2|+x>0 is

a)(-infinity,-2)U(2,infinity)

b)(-infinity,squre root of 2)U(square root of 2,infinity)

c)(-infinity,-1)U(1,infinity)

d)(square root of 2,infinity)

Asked by Abhilasha T. | 16 May, 2014, 12:09: AM
answered-by-expert Expert Answer
Consider,
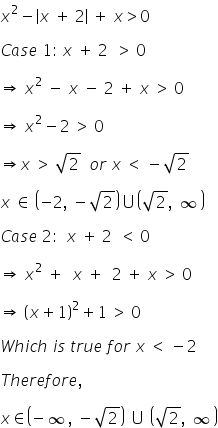
x squared minus open vertical bar x space plus space 2 close vertical bar space plus space x greater than 0 C a s e space 1 : space x space plus space 2 space space greater than space 0 rightwards double arrow space x squared space minus space x space minus space 2 space plus space x space greater than space 0 rightwards double arrow space x squared minus 2 space greater than space 0 rightwards double arrow x space greater than space square root of 2 space space o r space x space less than space minus square root of 2 x space element of space open parentheses minus 2 comma space minus square root of 2 close parentheses union open parentheses square root of 2 comma space infinity close parentheses space C a s e space 2 : space space x space plus space 2 space space less than space 0 rightwards double arrow space x squared space plus space space x space plus space space 2 space plus space x space greater than space 0 rightwards double arrow space open parentheses x plus 1 close parentheses squared plus 1 space greater than space 0 W h i c h space i s space t r u e space f o r space x space less than space minus 2 T h e r e f o r e comma space x element of open parentheses minus infinity comma space minus square root of 2 close parentheses space union space open parentheses square root of 2 comma space infinity close parentheses
Hence, the option 'A' is correct.
Answered by Avinash Soni | 16 May, 2014, 09:23: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
How to solve it ?  
question image
Asked by singhdivyang308 | 07 Feb, 2022, 09:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
ss
question image
Asked by indrajitchatterjee22092002 | 04 Aug, 2020, 10:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
{x^4+1/x(x^2+1)^2 dx  {1/sinx-sin2x dx
Asked by raghuvarandamodaran2002 | 28 Aug, 2019, 09:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration { 1/log x – 1/(log x )2}dx explain in great detail
Asked by haroonrashidgkp | 28 Oct, 2018, 01:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration log x dx/( 1 + log x )2 explain in great detail
Asked by haroonrashidgkp | 28 Oct, 2018, 01:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration ex (log x + 1/x2) dx  explain in great detail
Asked by haroonrashidgkp | 28 Oct, 2018, 01:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration ex (log x + 1/x2) dx 
Asked by haroonrashidgkp | 27 Oct, 2018, 05:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration xe2x dx/( 1 + 2x)2 explain in great detail
Asked by haroonrashidgkp | 27 Oct, 2018, 05:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration ( x + 1) ex dx/( x + 2)2 explain in great detail
Asked by haroonrashidgkp | 27 Oct, 2018, 05:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Integration  ex (  1 + sin x/1 + cos x ) dx  explain in great detail
Asked by haroonrashidgkp | 26 Oct, 2018, 09:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×