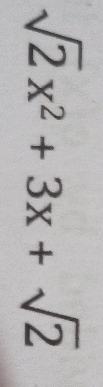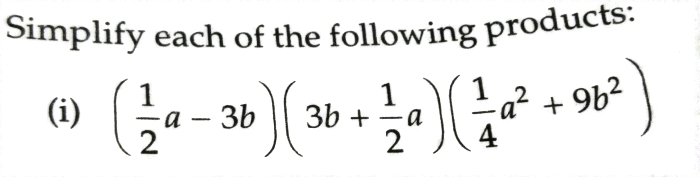CBSE Class 9 Answered
the remainder
Asked by manvendra singh | 19 Nov, 2013, 10:39: PM
Let p(x) = x 5 + kx 2
Consider division of (x 5 + kx 2) by (x – 1) (x – 2) (x – 3), then by division algorithm, there exists polynomials Q(x) and R(x) such that
x 5 + kx 2 = (x-1)(x-2)(x-3)Q(x) + R(x)
Here, 0 less than equal to deg R(x) < deg (x-1)(x-2)(x-3)
Let R(x) = ax2+bx+c
But it is given that remainder does not contain any therm of x 2
So, a = 0
This gives R(x) = bx+c
Therefore,
x 5 + kx 2 = (x-1)(x-2)(x-3)Q(x) + (bx+c) ... (1)
On putting x = 1, 2 and 3 in (1), we get
1 + k = b + c, 32 + 4k = 2b + c and 243 + 9k = 3b + c
On solving the equations, we get b = – 239, c = 150 and k = – 90
Hence, the value of k is – 90.
Answered by | 19 Nov, 2013, 11:19: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by durgavenkatlakshmi1 | 20 Mar, 2024, 03:56: PM
CBSE 9 - Maths
Asked by ammudeep0123 | 20 Mar, 2024, 07:13: AM
CBSE 9 - Maths
Asked by jaswanthsompi12345 | 19 Dec, 2023, 06:54: PM
CBSE 9 - Maths
Asked by rizwanmunna406 | 12 Dec, 2023, 10:09: PM
CBSE 9 - Maths
Asked by sathishdoddamudigere2 | 01 Nov, 2023, 06:53: PM
CBSE 9 - Maths
Asked by shambhushanker123 | 29 Oct, 2023, 08:36: PM