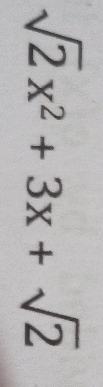CBSE Class 9 Answered
the remainder obtained when x^2006 is divided by x^2-1
Asked by amma95 | 14 Sep, 2009, 01:01: PM
Applying division algorithm when x^2006 is divided by x^2-1
x^2006 = (x^2-1)p(x)+r(x) ,where r(x) is a polynomial of degree atmost 1 ......(i)
let r(x)= Ax+B
(i) becomes
x^2006 = (x^2-1)p(x)+ Ax+B
substituting x=1 and x=-1 we get
A+B=1; A-B = 1 Solving we have A=0 B=0 so r(x) =1 option D isthe answer
Answered by | 21 Oct, 2009, 11:02: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by durgavenkatlakshmi1 | 20 Mar, 2024, 03:56: PM
CBSE 9 - Maths
Asked by ammudeep0123 | 20 Mar, 2024, 07:13: AM
CBSE 9 - Maths
Asked by jaswanthsompi12345 | 19 Dec, 2023, 06:54: PM
CBSE 9 - Maths
Asked by rizwanmunna406 | 12 Dec, 2023, 10:09: PM
CBSE 9 - Maths
Asked by sathishdoddamudigere2 | 01 Nov, 2023, 06:53: PM
CBSE 9 - Maths
Asked by shambhushanker123 | 29 Oct, 2023, 08:36: PM