Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

The ratio of the accelerations for a solid sphere(mass 'm' and radius 'r') rolling down an incline of angle 'theta' without slipping and slipping down the incline without rolling is:a)7:5b)5:7c)2:3d)2:5The above question was asked in AIPMT 2014.
Asked by Renuka Ganesh | 06 May, 2014, 09:49: PM
answered-by-expert Expert Answer
For slipping motion on an inclined plane the acceleration for a solid sphere making an angle θ  is given by
 
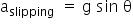
 straight a subscript slipping space end subscript space equals space straight g space sin space straight theta
For rolling motion of a sphere without slipping :
 
The acceleration of a sphere of mass m, radius r and moment of inertia I is 
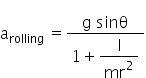
straight a subscript rolling space equals fraction numerator straight g space sinθ over denominator 1 plus begin display style straight I over mr squared end style end fraction
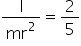
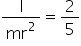
For a uniform sphere we know that straight I over mr squared equals 2 over 5
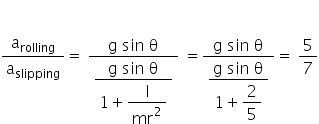
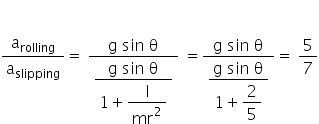
Substituting this  we get that the ratio straight a subscript rolling over straight a subscript slipping equals space fraction numerator straight g space sin space straight theta over denominator begin display style fraction numerator straight g space sin space straight theta over denominator 1 plus begin display style straight I over mr squared end style end fraction end style end fraction space equals fraction numerator straight g space sin space straight theta over denominator begin display style fraction numerator straight g space sin space straight theta over denominator 1 plus begin display style 2 over 5 end style end fraction end style end fraction equals space 5 over 7
Hence the ratio is 5:7 
Option b) is the correct answer.
Answered by Jyothi Nair | 07 May, 2014, 10:32: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
Respected Ma'am/Sir please clarify my doubt.
question image
Asked by pranavsrinivas82 | 08 Jan, 2024, 11:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
a block of mass m is pulled along a horizontal smooth surface by a rope of mass m force p applied at one end of rope force which the rope exert on block is
question image
Asked by rame123shshiv | 14 Nov, 2023, 06:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
second law of motion
Asked by kfcispuppy | 30 Sep, 2023, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Two blocks of mass m=5kg and M=10 kg are connected by a string passing over a pulley B as shown. Another string connects the centre of the pulley B to the floor and passes over another pulley A as shown. An upward force F is applied at the centre of pulley A. Both the pulleys are massless. Find the acceleration of both the blocks if 1) F=100N.  2)F=500N
question image
Asked by sakethrockzz007 | 14 Aug, 2023, 04:30: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A block of mass m is placed on a wedge as shown. Find difference between maximum and minimum (a(max) – a(min) ) horizontal rightward acceleration of wedge for which block remains at rest with respect to wedge. (A) 10g/9 (B) g/9 (C) g (D) None of these
question image
Asked by sahuaryanbro1.0 | 01 Jan, 2023, 10:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A force 50 N acts on a body for 10 sec.what will be the change in momentum
Asked by subhankarnanda123 | 20 Dec, 2022, 08:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
answer
question image
Asked by divyanshkr13 | 16 Jun, 2022, 10:25: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
find the velocity in rms
Asked by kashyspalbert91 | 11 Mar, 2022, 04:11: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
In the arrangement shown in the figure, a heavy pulley of mass M is suspended from a spring of stiffness constant K and the mass m is suspended from a string tightly wound on the pulley. If the mass m is given a small downward displacement and released, find the time period of small oscillations (Take pulley as Disc) and string does not slips on the pulley.
question image
Asked by alkrishna4652 | 24 Feb, 2022, 01:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
what is 2 law of motin
Asked by shreyamishra270304 | 04 Aug, 2021, 08:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×