CBSE Class 9 Answered
The radius of a spherical balloon increases from 3.5 cm to 4.2 cm as air is being pumped into it, find the ratio of surface areas of the balloon in the two cases.
Asked by Topperlearning User | 18 Oct, 2017, 03:20: PM
Case I
When radius (R) = 3.5 cm
Surface area (S1) = 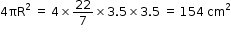
Case II: when radius (r) = 4.2 cm
Surface area (S2) = 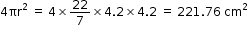
![]()
Therefore, S1: S2 =25:36
Answered by | 18 Oct, 2017, 05:20: PM
Concept Videos
CBSE 9 - Maths
Asked by manishgupta8980 | 15 Jul, 2022, 09:17: PM
CBSE 9 - Maths
Asked by nishimuthu21 | 05 Jul, 2020, 11:06: AM
CBSE 9 - Maths
Asked by dhanya_mk2000 | 21 Jan, 2020, 08:32: PM
CBSE 9 - Maths
Asked by ppiigoswami | 06 Dec, 2019, 08:53: PM
CBSE 9 - Maths
Asked by arajeevshashank | 29 Nov, 2019, 07:21: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Oct, 2017, 02:56: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Oct, 2017, 03:25: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Oct, 2017, 02:58: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Oct, 2017, 03:02: PM
CBSE 9 - Maths
Asked by Topperlearning User | 18 Oct, 2017, 03:03: PM





