Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

the perimeter of a triangular field is 280 dm. If two of its sides are 78 dm and 50 dm,find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Asked by saanvichhikara07 | 23 Sep, 2020, 08:10: AM
answered-by-expert Expert Answer
The question must be:
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution:
Let the third side be 'a'
Perimeter = 240
78+50+a = 240
a = 112
Using Heron's formula, we have
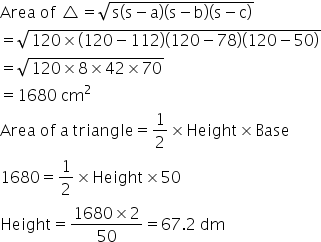
Area space of space triangle equals square root of straight s open parentheses straight s minus straight a close parentheses open parentheses straight s minus straight b close parentheses open parentheses straight s minus straight c close parentheses end root equals square root of 120 cross times open parentheses 120 minus 112 close parentheses open parentheses 120 minus 78 close parentheses open parentheses 120 minus 50 close parentheses end root equals square root of 120 cross times 8 cross times 42 cross times 70 end root equals 1680 space cm squared Area space of space straight a space triangle equals 1 half cross times Height cross times Base 1680 equals 1 half cross times Height cross times 50 Height equals fraction numerator 1680 cross times 2 over denominator 50 end fraction equals 67.2 space dm
Answered by Renu Varma | 23 Sep, 2020, 11:49: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
the perimeter of a triangular field is 280 dm. If two of its sides are 78 dm and 50 dm,find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Asked by saanvichhikara07 | 23 Sep, 2020, 08:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
A kite in the shape of a square with a diagonal 32 cm and Isis kilis triangle of base 8 cm and side 6 cm each is to be made of three different Shades as shown in the figure 12.17 how much paper of each shade has been used in it. Has been used in it.
question image
Asked by kirtisatpute995 | 14 Feb, 2020, 11:21: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
the side of a triangular field are 325m,300m,125m,.its area is
Asked by diptiadalj | 08 Nov, 2018, 10:17: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Find the area of triangle whose sides are 9 cm, 12 cm and 15 cm.
Asked by Topperlearning User | 16 May, 2014, 09:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Prove that area of a equilateral triangle with side ‘a' is .
Asked by Topperlearning User | 25 Jun, 2014, 01:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Find the perimeter of an equilateral triangle whose area is 4 square root of 3 space c m squared.
Asked by Topperlearning User | 31 Mar, 2014, 12:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
The perimeter of a triangle field is 450 m and its sides are in the ratio 13 : 12 : 5. Find the area of triangle.
Asked by Topperlearning User | 14 Mar, 2014, 08:07: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
The lengths of the sides of a triangle are 5 cm, 12 cm and 13 cm. Find the length of perpendicular from the opposite vertex to the side whose length is 13 cm.
Asked by Topperlearning User | 31 Mar, 2014, 12:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Find the percentage increase in the area of triangle if its each side is doubled.
Asked by Topperlearning User | 11 Feb, 2014, 12:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Find the area of a triangular field the lengths of whose sides are 275 m, 660 m and 715 m. What is the cost of cultivating the field at the rate of Rs. 200 per hectare?
Asked by Topperlearning User | 31 Mar, 2014, 01:04: PM
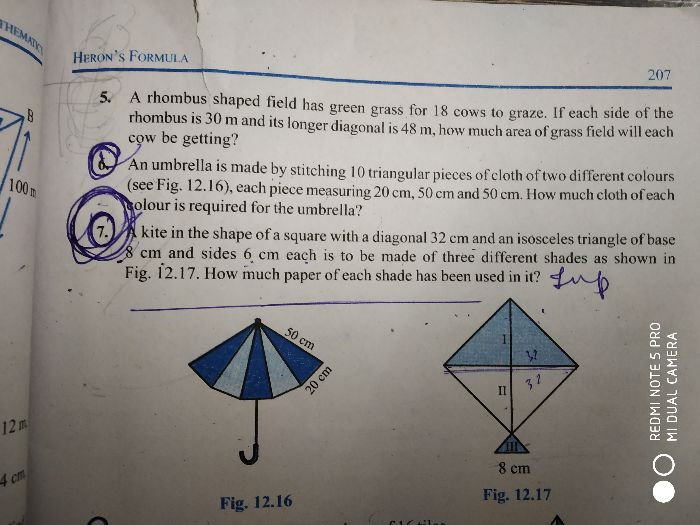
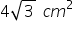ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×