Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

The locus of the centre of the circle which cuts off an intercept of constant length on the  x-axis and which passes through a fixed point on  the y- axis is ?

  

 

Asked by Malavika Umesh | 20 May, 2015, 05:53: PM
answered-by-expert Expert Answer
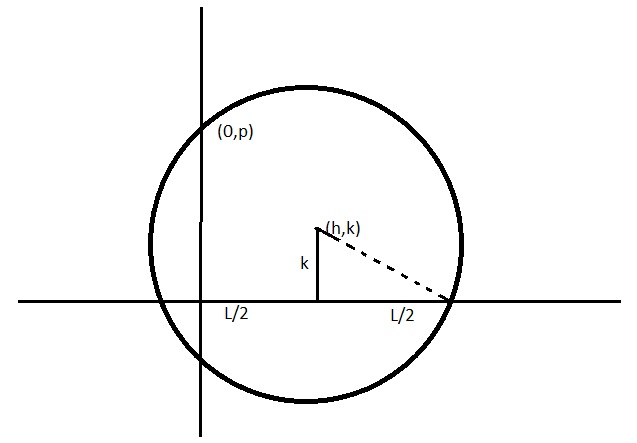
Refer to the figure above. 
Let the fixed point on Y-axis be (0,p). The length of intercept on X-axis be 'L'.
Let the coordinates of center be (h,k)
From the figure, the radius of the circle is 
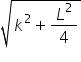
square root of k squared plus L squared over 4 end root
The equation of the circle can be written as
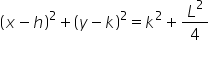
open parentheses x minus h close parentheses squared plus open parentheses y minus k close parentheses squared equals k squared plus L squared over 4
Since, the circle passes through the point (0,p), substituting the coordinates in the above equation, we get
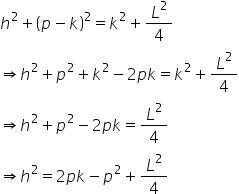
h squared plus open parentheses p minus k close parentheses squared equals k squared plus L squared over 4 rightwards double arrow h squared plus p squared plus k squared minus 2 p k equals k squared plus L squared over 4 rightwards double arrow h squared plus p squared minus 2 p k equals L squared over 4 rightwards double arrow h squared equals 2 p k minus p squared plus L squared over 4
 
Replacing (h,k) by (x,y), we get
x squared equals 2 p y minus p squared plus L squared over 4
This is an equation linear in 'y' and quadratic in 'x'. Hence, the locus will be a parabola.
Answered by satyajit samal | 21 May, 2015, 10:33: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
2 one
question image
Asked by dra | 24 Feb, 2024, 06:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find the coordinates of the centre of a circle passing through the points(0,0),(-2,1)and(-3,2).also , find its radius .
question image
Asked by shakyajayprakash2006 | 08 Jun, 2022, 05:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Examine whether the point (4, 5) lies outside or inside the circle of equation x^2+y^2-2x-3=0
Asked by sbipo2000 | 23 Feb, 2020, 03:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
SIR PLEASE HELP ME WITH THIS QUESTIONS : 1. Find the equation of the tangent to the circle x^2+y^2=16 drawn from the point (1,4). 2. How many triangles can be formed by joining any 3 of the 9 points when i) no 3 of them  are collinear? ii) 5 of them are collinear? 3. AB is a line of fixed length, 6 units, joining the points A(t,0) and B which lies on thepositive y axis. P is a point on AB distant 2 units from A. Express the coordinates of B and P in terms of t. Find the locus of P as t varies. 4. In a triangle ABC, (b^2 - c^2) / (b^2 + c^2) = sin(B - C) / sin(B + C), prove that it is either a right-angled or isoceles triangle.
Asked by kandappan | 08 Feb, 2020, 11:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
6
question image
Asked by gauravmore604 | 04 Nov, 2019, 03:31: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
The locus of point for which sum of the squares of distances from cordinate axes is 25 is
Asked by Tejravi969 | 19 Aug, 2019, 06:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
A stadium is in circular shape. Within the stadium some areas have been allotted for a hockey court and a javelin range, as given in the figure. Assume the shape of the hockey court and the javelin range to be square and triangle, resp. The curators would like to accommodate a few more sports in the stadium. Help them by measuring the unallocated region within the stadium.(the radius of the stadium is 200 mts.)  
Asked by rushabh1234 | 23 Jan, 2019, 08:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the equation of the circle with centre (-2,3) and radius 4.
Asked by Topperlearning User | 30 Apr, 2014, 11:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the centre and radius of the circle given by the equation (x + 5)2 + (y + 1 )2 = 9
Asked by Topperlearning User | 25 Apr, 2014, 09:39: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the co-ordinates of the centre and the radius of the circle given by the equation x2 + y2 + 6x - 8y - 24 = 0.
Asked by Topperlearning User | 25 Apr, 2014, 09:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×