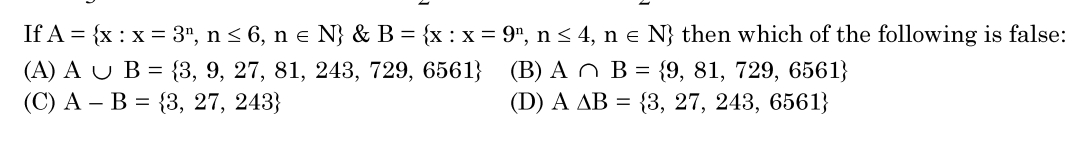CBSE Class 11-science Answered
the empty set belongs to set A.true or false and how?
Asked by Bholanath Beura | 04 Apr, 2013, 06:40: PM
Expert Answer
Empty/ Null set is a subset of every set.
The proof is as follows:
Let A be any set.
Now, to show the empty set phi is a subset of A, we have to show that:
All elements of phi are in A.
There is no element in phi which is not in A. If there was indeed any, then the null set would contain elements, which goes against its definition.
Hence, Empty/ Null set is a subset of every set.
Answered by | 05 Apr, 2013, 10:01: AM
Concept Videos
-
Types of sets and its representation
Types of sets and describe two forms of set representation. -
Subsets and Supersets
This video covers the definition of subsets and supersets of a set and also... -
Representing the union and intersection of sets
Venn diagrams. Represent the union and intersection of sets with the help o... -
Algebra of Sets
This video explains the concept of the difference of two given sets and rep... -
Counting Theorems ...
This video explains the application of set theory and Venn diagram to solve...
CBSE 11-science - Maths
Asked by parvanipatil09 | 29 Mar, 2024, 10:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by divyanshtikkiwal6 | 23 Feb, 2024, 07:44: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pranavsrinivas82 | 14 Jan, 2024, 07:45: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pranavsrinivas82 | 10 Jan, 2024, 08:45: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by naiduuofficial | 06 Jan, 2023, 07:49: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by anjaneyagadgil04 | 05 Jan, 2023, 12:16: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by bangtan7hybe | 18 Sep, 2022, 06:36: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by kdimple765 | 24 Jun, 2022, 04:22: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by arjunsah797 | 03 Mar, 2022, 06:04: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by krishkhare04 | 03 Feb, 2022, 02:35: PM
ANSWERED BY EXPERT
