Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

the diagonals of a quadrilateral PQRS intersect each other at point O such that PO/QR=OQ/OS.Prove that PQRS is atrapezium
 
Asked by Pawan | 24 Aug, 2014, 02:53: PM
answered-by-expert Expert Answer
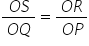
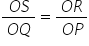
A quadrilateral PQRS whose diagonals PR and QS intersect each other at O such that fraction numerator O S over denominator O Q end fraction equals fraction numerator O R over denominator O P end fraction
To prove : Quadrilateral PQRS is a trapezium
Construction : Draw OT || PQ meeting PS at T.

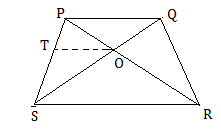
Proof : In 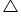trianglePSR, OT || SR....(i)
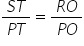fraction numerator S T over denominator P T end fraction equals fraction numerator R O over denominator P O end fraction                                         (By Basic proportionaity theorem)..........(ii)
Also, 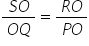fraction numerator S O over denominator O Q end fraction equals fraction numerator R O over denominator P O end fraction                                (Given)...........(iii)
From (ii) and (iii), we get

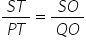
fraction numerator S T over denominator P T end fraction equals fraction numerator S O over denominator Q O end fraction
 SR || OT                                                   (Converse of Basic proportionality theorem)......(iv) 
From (i) and (iv), we get
SR || PQ
Hence quadrilateral PQRS is trapezium.

 

Answered by Anuja Salunke | 25 Aug, 2014, 10:07: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
give answer
question image
Asked by kumarjogesh746 | 28 Dec, 2022, 07:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Answer of the question given below
question image
Asked by bhu.joshi54 | 04 Jul, 2022, 08:18: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Two angles of a triangle are 70° and 80° The vertices of the triangle are on a circle of radius 3.5cm construct the triangle.
Asked by lijimoljayan | 12 Sep, 2021, 06:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 05 Sep, 2020, 10:34: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Using Basic Proportionality Theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. [NCERT]
question image
Asked by kundanstm3963 | 26 Apr, 2020, 09:27: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
what is Thales therom
Asked by sharmaanjali06959 | 20 Dec, 2019, 09:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in the figure, if de parallel bc and ad = 4x -3 ae = 8x -7 , bd = 3x- 1 and ce = 5x -2fi x.d--
Asked by manshisinha117 | 12 Nov, 2019, 04:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In the figure of ∆ABC ,DC ||AB. If AD = 2x ,DC = X +3, BC = 2x-1 and CE =X, then find the value of X.
Asked by sumitkain2016 | 26 Feb, 2019, 01:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In three line segments OA, OB and OC,points L,M,Nrespectively are so shosen that LM ll AB and MN ll BC but neither of L, M nor of A,B,C are collinear. Show that LN ll AC.
Asked by gpnkumar0 | 07 Mar, 2018, 09:37: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
E and F are points on the sides PQ and PR respectively of a PQR.  State whether EF || QR. PE = 3.9cm, EQ = 3cm, PF =3.6cm and FR = 2.4cm.
Asked by Topperlearning User | 26 Jul, 2017, 01:40: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×