The coeffiucient of x^k ( 0<=k<= n )in the expansion of E = 1 + (1+x) + (1 + x)^2 + ........ + ( 1 + x )^n is ... . Calculate the same.
Asked by sudhanshubhushanroy | 6th Nov, 2017, 09:04: PM
Expert Answer:
Answered by Sneha shidid | 11th Dec, 2017, 02:14: PM
Concept Videos
- 17th sum
- What is the use of Binomial Theorem?
- Write the statement of Binomial Theorem for positive integral indices.
- For any natural number n, Prove that
.
- Expand
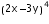by using binomial expansion.
- Using binomial theorem, evaluate
.
- Find the general term in the expansion of
:
- Find the middle term in the expansion of
:
- Find the middle term in the expansion of
.
- Find the term independent of x in the expansion of
:
Kindly Sign up for a personalised experience
- Ask Study Doubts
- Sample Papers
- Past Year Papers
- Textbook Solutions
Sign Up
Verify mobile number
Enter the OTP sent to your number
Change