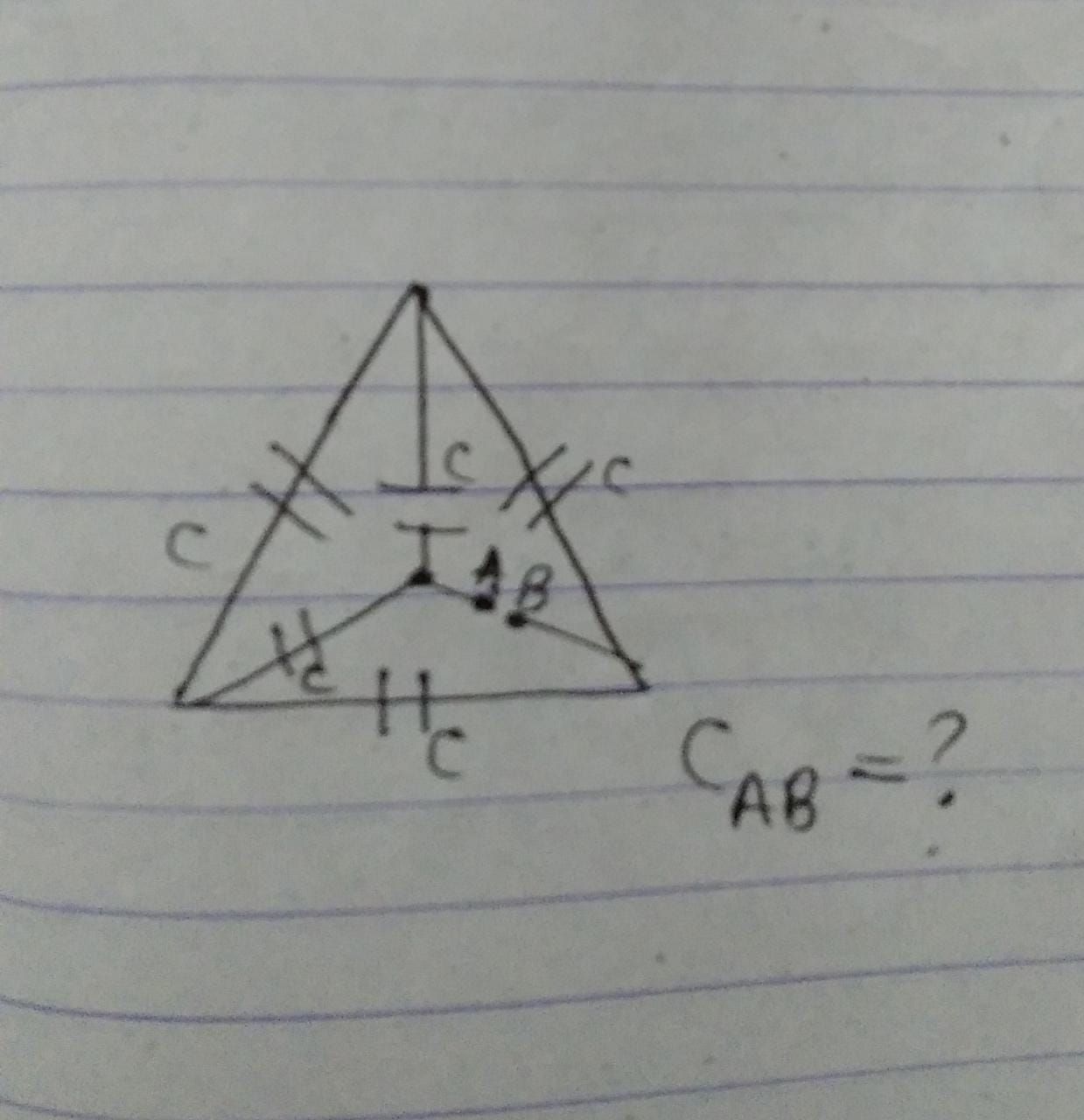The classic resistor cube.

This is an oldie, but still a goodie.

Twelve identical resistors of resistance r are soldered together in a cubic network.

(a) What is the resistance measured with an ohmmeter between A and C?

(b) What is the resistance between A and B?

(c) What is the resistance between A and D?

Give all answers in terms of r.

(a) 

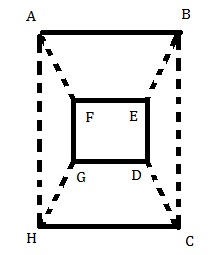
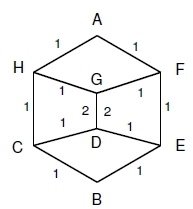
Let consider a square with corners ABCH. Connect F, E, D, G to it respectively.

Since BE and GH provides the symmetry circuit. Hence, no current through this branch.

There are three parallel branches between BC

In ABC and AHC branches two resistance are in series each i.e. 2r and branch FES is parallel with FGD therefore equivalent resistance between them is r.

From this we can see that, the inner branch has resistance is 3r.

Total resistance between AC is,

 

(b) 

 

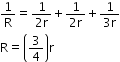
From the figure we have,

Branch HC in parallel with 4r which gives 4/5 r.

IF we see from A to B along left, resistance between them is 14/5r. This is parallel with other side and we get 7/5r.

7/5r is parallel with r of AB. Hence, resistance across AB is (7/12)r

(c)Now the current I at node A splits into three equal parts I/3.

The current I/3 at node B splits into two equal parts I/6.

Two currents I/6 at node C add to a current I/3 in resistor CD.

Let, the potential across AB is V,

then by Ohm's law, the potential across BC is V/2 and the potential across CD is V.

Taking the sum of potentials AB, BC, CD. Therefore,  The potential A to D is then 5/2 V.

I/3 = V/R     ( where R is one resistor).

 So I = 3V/R and R = 3V/I.

The resistance of the cube from A to D from one end to other end is:

 R = (5/2)V/(3V/R)= (5/6)R